题目内容
某车间共有八位工人,为了保障安全生产,每月1号要从中选取四名工人参加同样的技能测试,每个工人通过每次测试的概率是
.甲从事的岗位比较特殊,每次他都必须参加技能测试,另外乙和丙从事同一岗位的工作,所以他们不能同时离开岗位参加技能测试.
(1)每次选拔时,共有多少种选取方式?
(2)工厂规定:工人连续2次没通过测试,则被撤销上岗资格.求甲工人恰好参加4次测试后被撤销上岗资格的概率.
| 3 |
| 4 |
(1)每次选拔时,共有多少种选取方式?
(2)工厂规定:工人连续2次没通过测试,则被撤销上岗资格.求甲工人恰好参加4次测试后被撤销上岗资格的概率.
考点:概率的应用
专题:计算题,概率与统计
分析:(1)分两类:若乙、丙均不选,若乙、丙中选一个,由条件结合分类相加,分步相乘原理,即可得到;
(2)记事件A为:“甲工人恰好参加4次测试后后被撤销上岗资格”,记A1为“甲第一、二次通过,第三、四次未通过测试”,运用概率的乘法公式求出P(A1),记A2为“甲第一次未通过,第二次通过,第三、四次未通过测试”,求得P(A2),由于A1,A2互斥,则P(A)=P(A1)+P(A2),即可得到.
(2)记事件A为:“甲工人恰好参加4次测试后后被撤销上岗资格”,记A1为“甲第一、二次通过,第三、四次未通过测试”,运用概率的乘法公式求出P(A1),记A2为“甲第一次未通过,第二次通过,第三、四次未通过测试”,求得P(A2),由于A1,A2互斥,则P(A)=P(A1)+P(A2),即可得到.
解答:
解:(1)若乙、丙均不选,甲必须选,从剩下的5人中选3人,有
=10种;
若乙、丙中选一个,则有
=20种,
故每次选拔时,共有30种选取方式;
(2)记事件A为:“甲工人恰好参加4次测试后后被撤销上岗资格”,
记A1为“甲第一、二次通过,第三、四次未通过测试”,
则P(A1)=
×
×
×
=
,
记A2为“甲第一次未通过,第二次通过,第三、四次未通过测试”,
则P(A2)=
×
×
×
=
,
由于A1,A2互斥,
则P(A)=P(A1)+P(A2)=
=
.
故甲工人恰好参加4次测试后被撤销上岗资格的概率为
.
| C | 3 5 |
若乙、丙中选一个,则有
| C | 1 2 |
| •C | 2 5 |
故每次选拔时,共有30种选取方式;
(2)记事件A为:“甲工人恰好参加4次测试后后被撤销上岗资格”,
记A1为“甲第一、二次通过,第三、四次未通过测试”,
则P(A1)=
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 256 |
记A2为“甲第一次未通过,第二次通过,第三、四次未通过测试”,
则P(A2)=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 256 |
由于A1,A2互斥,
则P(A)=P(A1)+P(A2)=
| 3+9 |
| 256 |
| 3 |
| 64 |
故甲工人恰好参加4次测试后被撤销上岗资格的概率为
| 3 |
| 64 |
点评:本题考查排列组合和概率的应用题,考查两个计数原理的运用,独立事件同时发生的概率的公式以及互斥事件发生的概率,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
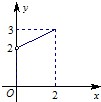 已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.
已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示. 高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为1,2,…,7的球槽内.某高三同学试验1000次,掉入各球槽的个数统计如下:
高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为1,2,…,7的球槽内.某高三同学试验1000次,掉入各球槽的个数统计如下: