题目内容
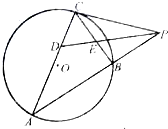如图，PC是圆O的切线，切点为C，直线PA与圆O交于两点A、B，∠APC的平分线分别交弦CA、CB于两点D、E，已知PC=3，PB=2，则| PE |
| PD |
考点：与圆有关的比例线段
专题：直线与圆
分析：由∠APC的平分线分别交弦CA、CB于两点D、E，得∠CPE=∠APD，由PC是圆O的切线，切点为C，得∠BCP=∠BAC，从而△PCE∽△ADP，由此得∠PDC=∠PEB，从而△EBP∽△DCP，由此能求出
=
=
．
| PE |
| PD |
| PB |
| PC |
| 2 |
| 3 |
解答：
解：∵∠APC的平分线分别交弦CA、CB于两点D、E，
∴∠CPE=∠APD，
∵PC是圆O的切线，切点为C，
∴∠BCP=∠BAC，
∴△PCE∽△ADP，
∴∠ADP=∠PEC，
∴∠PDC=∠PEB，
∴△EBP∽△DCP，
∴
=
=
．
故答案为：
．
∴∠CPE=∠APD，
∵PC是圆O的切线，切点为C，
∴∠BCP=∠BAC，
∴△PCE∽△ADP，
∴∠ADP=∠PEC，
∴∠PDC=∠PEB，
∴△EBP∽△DCP，
∴
| PE |
| PD |
| PB |
| PC |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查圆中两线段的比值的求法，是中档题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
已知x＞-1，则函数y=x+
的最小值为（ ）
| 1 |
| x+1 |
| A、-1 | B、0 | C、1 | D、2 |
若非空集合A、B满足A?B，U为全集，则下列集合为空集的是（ ）
| A、A∩B |
| B、A∩（∁UB） |
| C、A∪（∁UB） |
| D、（∁UA）∪（∁UB） |