题目内容
| ∫ | 2 1 |
| 1 |
| x |
考点:定积分
专题:计算题,导数的概念及应用
分析:根据积分公式,即可得到结论
解答:
解:
(
+ex)dx=(lnx+ex)
=
+e2-e=e2-e+
故答案为:e2-e+
| ∫ | 2 1 |
| 1 |
| x |
| | | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:e2-e+
| 1 |
| 2 |
点评:本题主要考查积分的计算,要求熟练掌握常见函数的积分公式.

练习册系列答案
相关题目
若非空集合A、B满足A?B,U为全集,则下列集合为空集的是( )
| A、A∩B |
| B、A∩(∁UB) |
| C、A∪(∁UB) |
| D、(∁UA)∪(∁UB) |
函数f(x)=(
)x-log2x,正实数a,b,c满足a<b<c且f(a)•f(b)•f(c)<0.若实数d是方程f(x)=0的一个解,那么下列四个判断:①d<a;②d>a;③d>c;④d<c中有可能成立的个数为( )
| 1 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
不等式|5x-x2|<6的解集为( )
| A、{x|x<2或x>3} |
| B、{x|-1<x<2或3<x<6} |
| C、{x|-1<x<6} |
| D、{x|2<x<3} |
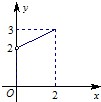 已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.
已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.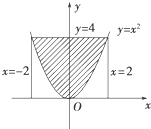 如图在区域Ω={(x,y)|-2≤x≤2,0≤y≤4}中随机撒豆子,豆子落在图中阴影部分内的概率为
如图在区域Ω={(x,y)|-2≤x≤2,0≤y≤4}中随机撒豆子,豆子落在图中阴影部分内的概率为 高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为1,2,…,7的球槽内.某高三同学试验1000次,掉入各球槽的个数统计如下:
高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为1,2,…,7的球槽内.某高三同学试验1000次,掉入各球槽的个数统计如下: