题目内容
8．已知α是第二象限角，那么$\frac{α}{2}$是（ ）| A． | 第一象限角 | B． | 第二象限角 | ||
| C． | 第一或第二象限角 | D． | 第一或第三象限角 |
分析 写出终边相同的角的集合，然后求出$\frac{α}{2}$所在象限即可．
解答 解：∵α是第二象限角，
∴$\frac{π}{2}$+2kπ＜α＜π+2kπ，k∈Z，
∴$\frac{π}{4}$+kπ＜$\frac{α}{2}$＜$\frac{π}{2}$+kπ，k∈Z，
当k为偶数时，$\frac{α}{2}$是第一象限角，k为奇数时，$\frac{α}{2}$是第三象限角，
∴$\frac{α}{2}$是第一或第三象限角．
故选：D．
点评 本题考查象限角、轴线角，注意k为奇数、偶数的情况，由此可以确定α在其它象限的情况，是基础题．
练习册系列答案
相关题目
19．已知曲线C：$y=\frac{1}{3}{x^3}-{x^2}-4x+1$，直线l：x+y+2k-1=0，当x∈[-3，3]时，直线l恒在曲线C的上方，则实数k的取值范围是（ ）
| A． | $k＞-\frac{5}{6}$ | B． | $k＜-\frac{5}{6}$ | C． | $k＜-\frac{3}{4}$ | D． | $k＞-\frac{3}{4}$ |
3．已知两个等差数列{an}和{bn}的前n项和分别为An和Bn，且$\frac{A_n}{B_n}=\frac{7n+57}{n+3}$，则使得$\frac{a_n}{b_n}$为整数的正整数n的个数是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
13．已知函数f（x）=cosx，若存在实数x1，x2，…，xm（m≥2，m∈N）满足条件0≤x1＜x2＜…＜xm≤6π，且|f（x1）-f（x2）|+…+|f（xm-1）-f（xm）|=12，则m的最小值为（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
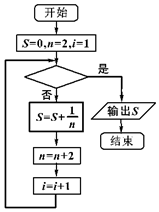如图，给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图，其中判断框内应填入的条件是（ ）