题目内容
13.已知函数f(x)=cosx,若存在实数x1,x2,…,xm(m≥2,m∈N)满足条件0≤x1<x2<…<xm≤6π,且|f(x1)-f(x2)|+…+|f(xm-1)-f(xm)|=12,则m的最小值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 根据余弦函数的性质可知|f(xi)-f(xi+1)|≤2,故而当|f(xi)-f(xi+1)|=2时,m取得最小值.
解答 解:∵-1≤f(x)≤1,
∴|f(xi)-f(xi+1)|≤2,i=1,2,3…,
且在[0,6π]上只有6对实数,使得|f(xi)-f(xi+1)|=2,
此时令xi=(i-1)π,i=1,2,3,…,7,则|f(x1)-f(x2)|+…+|f(xm-1)-f(xm)|=12.
∴故m=7.
故选B.
点评 本题考查了余弦函数的性质,属于中档题.

练习册系列答案
相关题目
4.sin$\frac{π}{6}$的值等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
8.已知α是第二象限角,那么$\frac{α}{2}$是( )
| A. | 第一象限角 | B. | 第二象限角 | ||
| C. | 第一或第二象限角 | D. | 第一或第三象限角 |
18.已知点A(0,-1)是抛物线C:x2=2py(p>0)准线上的一点,点F是抛物线C的焦点,点P在抛物线C上且满足|PF|=m|PA|,当m取最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{3}$+1 |
5.证明不等式$\sqrt{a+1}-\sqrt{a}<\sqrt{a-1}-\sqrt{a-2}({a≥2})$所用的最适合的方法是( )
| A. | 分析法 | B. | 综合法 | C. | 反证法 | D. | 合情推理 |
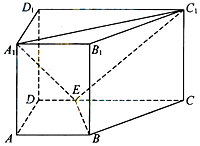 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3