Question

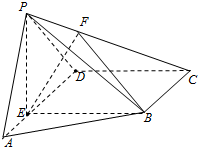如图，在四棱锥P=ABCD中，E为AD上一点，面PAD⊥面ABCD，四边形BCDE为矩形∠PAD=60°，PB=2

3

，PA=ED=2AE=2．
（Ⅰ）已知

PF

=λ

PC

（λ∈R），且PA∥面BEF，求λ的值；
（Ⅱ）求证：CB⊥平面PEB．

Answer 1

考点：直线与平面垂直的判定,直线与平面平行的判定

专题：综合题,空间位置关系与距离

分析：（Ⅰ）连接AC交BE于点M，连接FM，利用线面平行的性质，结合比例线段，即可求λ的值；
（Ⅱ）证明CB⊥平面PEB，只需证明CB垂直于平面PEB内的两条相交直线．

解答： （Ⅰ）解：连接AC交BE于点M，连接FM．
∵PA∥面BEF，
∴FM∥AP                …（2分）
∵EM∥CD，∴

AM

MC

=

AE

ED

=

1

2

∵FM∥AP，
∴

PF

FC

=

AM

MC

=

1

2

∴λ=

1

3

       …（6分）
（Ⅱ）证明：∵AP=2，AE=1，∠PAD=60°，∴PE=

3

，
∴PE⊥AD…（8分）
又面PAD⊥面ABCD，且面PAD∩面ABCD=AD，
∴PE⊥面ABCD，∴PE⊥CB，
又BE⊥CB，且PE∩BE=E，
∴CB⊥平面PEB．   …（12分）

点评：本题考查线面平行的性质，考查线面垂直的判断，考查学生分析解决问题的能力，属于中档题．