题目内容
已知
=（1，1），
=（sin（α-
），cosα+
）），且
∥
，求sin2α+2sinαcosα的值．
| a |
| b |
| π |
| 3 |
| π |
| 3 |
| a |
| b |
考点：三角函数的化简求值,平面向量共线（平行）的坐标表示
专题：三角函数的求值
分析：通过向量的平行．推出角的三角函数的关系，求出tanα=1，利用1的代换求解表达式的值．
解答：
解：∵
∥
∴cos(α+
)-sin(α-
)=0
∴sinα=cosα，
∴tanα=1
∴sin2α+2sinαcosα
=
=
=
．
| a |
| b |
∴cos(α+
| π |
| 3 |
| π |
| 3 |
∴sinα=cosα，
∴tanα=1
∴sin2α+2sinαcosα
=
| sin2α+2sinαcosα |
| cos2α+sin2α |
=
| tan2α+2tanα |
| 1+tan2α |
=
| 3 |
| 2 |
点评：本题考查三角函数的化简求值，向量的平行关系，值域“1”的代换是解题的关键，是基础题．
练习册系列答案
相关题目
直线2x-3y+m=0和3x+2y+n=0的位置关系是（ ）
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、不能确定 |
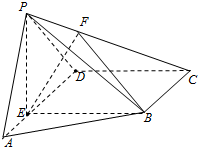如图，在四棱锥P=ABCD中，E为AD上一点，面PAD⊥面ABCD，四边形BCDE为矩形∠PAD=60°，PB=2
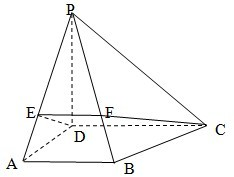已知四棱锥P-ABCD，PD⊥面ABCD，AB∥DC，AD⊥DC，AD=