题目内容
数列{an}满足a1=1,an+1=
(n∈N+)
(1)证明:数列{
}是等差数列;
(2)求数列{an}的通项公式an;
(3)设bn=(2n-1)(n+1)an,求数列{bn}的前n项和Sn.
| 2n+1an |
| an+2n |
(1)证明:数列{
| 2n |
| an |
(2)求数列{an}的通项公式an;
(3)设bn=(2n-1)(n+1)an,求数列{bn}的前n项和Sn.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)根据等差数列的定义即可证明:数列{
}是等差数列;
(2)利用(1)求出
的通项公式,即可求数列{an}的通项公式an;
(3)利用错位相减法即可求数列{bn}的前n项和Sn
| 2n |
| an |
(2)利用(1)求出
| 2n |
| an |
(3)利用错位相减法即可求数列{bn}的前n项和Sn
解答:
解:(1)取倒数得:
=
+
,两边同乘以2n+1得:
=1+
,
所以数列{
}是以
=2为首项,以1为公差的等差数列.
(2)∵{
}是以
=2为首项,以1为公差的等差数列.,
∴
=
+(n-1)×1,
即an=
.
(3)由题意知:bn=(2n-1)•2n则前n项和为:Sn=1×2+3×22+5×23+…+(2n-1)×2n,
2Sn=1×22+3×23+5×24+…(2n-1)×2n+1,
由错位相减得:-Sn=2+2(22+23+…+2n)-(2n-1)×2n+1,
∴Sn=(2n-3)×2n+1+6.
| 1 |
| an+1 |
| 1 |
| 2n+1 |
| 1 |
| 2an |
| 2n+1 |
| an+1 |
| 2n |
| an |
所以数列{
| 2n |
| an |
| 21 |
| a1 |
(2)∵{
| 2n |
| an |
| 21 |
| a1 |
∴
| 2n |
| an |
| 2 |
| 1 |
即an=
| 2n |
| n+1 |
(3)由题意知:bn=(2n-1)•2n则前n项和为:Sn=1×2+3×22+5×23+…+(2n-1)×2n,
2Sn=1×22+3×23+5×24+…(2n-1)×2n+1,
由错位相减得:-Sn=2+2(22+23+…+2n)-(2n-1)×2n+1,
∴Sn=(2n-3)×2n+1+6.
点评:本题主要考查数列的通项公式以及数列求和,利用错位相减法是解决本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
若A(1,-2,1),B(4,2,3),C(6,-9,4),则△ABC的形状是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
直线2x-3y+m=0和3x+2y+n=0的位置关系是( )
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、不能确定 |
用数学归纳法证明1+a+a2+…+an+1=
(a≠1,n∈N*),在验证当n=1时,等式左边应为( )
| 1-an+2 |
| 1-a |
| A、1 |
| B、1+a |
| C、1+a+a2 |
| D、1+a+a2+a3 |
 如图,已知多面体ABC-DEFG,三条棱AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.
如图,已知多面体ABC-DEFG,三条棱AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.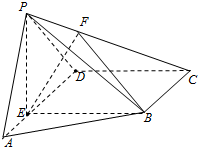 如图,在四棱锥P=ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2
如图,在四棱锥P=ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2