题目内容

求和：Sn=
1
2
+
3
4
+
5
8
+
7
16
+…+
2n-1
2n
．
考点：数列的求和
专题：等差数列与等比数列
分析：利用错位相减法即可得到结论．
解答： 解：因为Sn=
1
2
+
3
4
+
5
8
+
7
16
+…+
2n-1
2n
，
所以
1
2
Sn=
1
4
+
3
8
+
5
16
+…+
2n-3
2n
+
2n-1
2n+1
，
两式相减得：
1
2
Sn=
1
2
+
2
4
+
2
8
+
2
16
+…+
2
2n
-
2n-1
2n+1
=
1
2
+
1
2
(1-
1
2n-1
)
1-
1
2
-
2n-1
2n+1
，
则Sn=3-
2n+3
2n
．
点评：本题主要考查数列求和，利用错位相减法是解决本题的关键．
练习册系列答案
相关题目
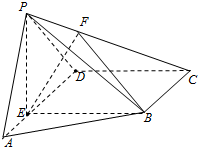如图，在四棱锥P=ABCD中，E为AD上一点，面PAD⊥面ABCD，四边形BCDE为矩形∠PAD=60°，PB=2
3
，PA=ED=2AE=2．
（Ⅰ）已知
PF
=λ
PC
（λ∈R），且PA∥面BEF，求λ的值；
（Ⅱ）求证：CB⊥平面PEB．
设f（x）=（k+1）x2-（2k+1）x+1，x∈R．
（1）若f（x）＞0恒成立，求实数k的取值范围；
（2）当-1＜k＜0时，解不等式f（x）＞0．
在平面直角坐标系xOy中，已知动点P（x，y）（y≤0）到点F（0，2）的距离为d1，到x轴的距离为d2，且d1-d2=2．
（Ⅰ）求点P的轨迹E的方程；
（Ⅱ）若直线l斜率为1且过点（1，0），其与轨迹E交于点M、N，求|MN|的值．
已知函数f（x）=2
3
sinxcosx+2cos2x-1
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求f（x）在区间[-
π
6
，
π
4
]上的最大值和最小值．
已知数列{an}、{bn}满足a1=2，an-1=an（an+1-1），bn=an-1，数列{bn}的前n项和为Sn，n∈N*．
（1）证明数列{
1
bn
}为等差数列，并求数列{bn}的通项公式；
（2）用数学归纳法证明：对任意的n∈N*，有1+
n
2
≤S2n≤
1
2
+n成立．
已知数列{an}满足a1=1，an+1=2an+1（n∈N*）．
（1）求数列{an}的通项公式；
（2）设Sn为数列{
2n
an+1
}的前n项和，求Sn．
（3）证明：
1
a1
+
1
a2
+
1
a3
+…+
1
an+1
＜
5
3
（n∈N*）．
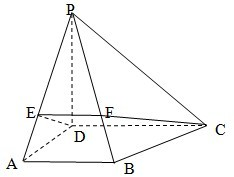已知四棱锥P-ABCD，PD⊥面ABCD，AB∥DC，AD⊥DC，AD=
2
，CD=4，PD=2，E为AP上一点，DE⊥AP，F是平面DEC与BP的交点．
（Ⅰ）求证：EF∥AB；
（Ⅱ）求证：AP⊥面EFCD；
（Ⅲ）求PC与面EFCD所成角的正弦值．
已知函数f（x）=-
1
3
x3+
a
2
x2-2x，g（x）=
1
3
x3-
a
2
x2+（a+2）x+
a+1
x
-lnx，（a∈R）
（Ⅰ）当a=3时，x∈[
3
2
，2]，求函数f（x）的最大值；
（Ⅱ）当a≥-1时，讨论函数F（x）=f（x）+g（x）的单调性；
（Ⅲ）若过点（0，-
1
3
）可作函数y=f（x）图象的三条不同切线，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网