题目内容
函数f（x）=ex+x2-2的零点的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：令f（x）=0，得到ex=-x2+2，作出函数y=ex，和y=-x2+2的图象，利用数形结合即可得到结论．
解答：
解：令f（x）=0，得到ex=-x2+2，作出函数y=ex，和y=-x2+2的图象如图：
由图象可知两个图象的交点公式为2个，
即函数f（x）=ex+x2-2的零点的个数为2个，
故选：B．
解：令f（x）=0，得到ex=-x2+2，作出函数y=ex，和y=-x2+2的图象如图：由图象可知两个图象的交点公式为2个，
即函数f（x）=ex+x2-2的零点的个数为2个，
故选：B．
点评：本题主要考查函数零点公式的判定，利用函数和方程之间的关系转化为两个图象的交点问题是解决本题的关键．
练习册系列答案
初中暑期衔接系列答案
相关题目
顶点在原点，对称轴是y轴，并且顶点与焦点的距离为3的抛物线的标准方程为（ ）
| A、x2=±3y |
| B、y2=±6x |
| C、x2=±12y |
| D、x2=±6y |
若A（1，-2，1），B（4，2，3），C（6，-9，4），则△ABC的形状是（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
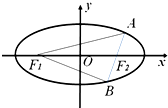已知F1，F2为椭圆的两个焦点，|F1F2|=6，如图△AF1B的顶点A、B在椭圆上，F2在边AB上，其周长为20，则椭圆的离心率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
某考察团对全国10大城市进行职工人均工资水平x（千元）与居民人均消费水平y（千元）统计调查发现，y与x具有相关关系，回归方程为
=0.66x+1.562．若某城市居民人均消费水平为7.675（千元），估计该城市人均消费额占人均工资收入的百分比约为（ ）
 |
| y |
| A、83% | B、72% |
| C、67% | D、66% |
若直线y=m与y=3x-x3的图象有三个不同的交点，则实数m的取值范围为（ ）
| A、-2＜m＜2 |
| B、-2≤m≤2 |
| C、m＜-2或m＞2 |
| D、m＜-2或m≥2 |
直线2x-3y+m=0和3x+2y+n=0的位置关系是（ ）
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、不能确定 |
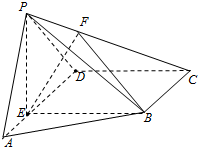如图，在四棱锥P=ABCD中，E为AD上一点，面PAD⊥面ABCD，四边形BCDE为矩形∠PAD=60°，PB=2