题目内容
 如图四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4
如图四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4| 2 |
| 2 |
(Ⅰ)求证:PQ∥平面BCE;
(Ⅱ)求证:AM⊥平面BCM.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)根据M为EF中点,EF=4
,进而可知EM,进而可知AB∥EM,AB=EM,推断出四边形ABEM为平行四边形,连接AE,根据P是BM中点,推断出P是AE的中点,Q为AC中点,推断出在△AEC中,PQ∥EC,进而利用线面平行判定定理推断出PQ∥平面BCE.
(Ⅱ)由(Ⅰ)知:AM=BE=2,同理可得:BM=AF=2,又AB=2
,推断出AB2=AM2+BM2,进而可知AM⊥BM,根据四边形ABCD为矩形,推断出BC∥AD,又AD⊥平面ABEF,推断出BC⊥平面ABEF,根据线面垂直的性质可知BC⊥AM,利用线面垂直的判定定理推断出AM⊥平面BCM.
| 2 |
(Ⅱ)由(Ⅰ)知:AM=BE=2,同理可得:BM=AF=2,又AB=2
| 2 |
解答:
解:(Ⅰ)∵M为EF中点,EF=4
,
∴EM=2
,
∴AB∥EM,AB=EM,
∴四边形ABEM为平行四边形,
连接AE,
∵P是BM中点,
∴P是AE的中点,
∵Q为AC中点,
∴在△AEC中,PQ∥EC,
∵PQ?平面BCE,
∴PQ∥平面BCE.
(Ⅱ)由(Ⅰ)知:AM=BE=2,
同理可得:BM=AF=2,
又AB=2
,
∴AB2=AM2+BM2,
∴AM⊥BM,
∵四边形ABCD为矩形,
∴BC∥AD,
又AD⊥平面ABEF,
∴BC⊥平面ABEF,
∴BC⊥AM,
又BC∩BM=B,
∴AM⊥平面BCM.
| 2 |
∴EM=2
| 2 |
∴AB∥EM,AB=EM,
∴四边形ABEM为平行四边形,
连接AE,
∵P是BM中点,
∴P是AE的中点,
∵Q为AC中点,
∴在△AEC中,PQ∥EC,
∵PQ?平面BCE,
∴PQ∥平面BCE.
(Ⅱ)由(Ⅰ)知:AM=BE=2,
同理可得:BM=AF=2,
又AB=2
| 2 |
∴AB2=AM2+BM2,
∴AM⊥BM,
∵四边形ABCD为矩形,
∴BC∥AD,
又AD⊥平面ABEF,
∴BC⊥平面ABEF,
∴BC⊥AM,
又BC∩BM=B,
∴AM⊥平面BCM.
点评:本题主要考查了线面平行和线面垂直的判定定理的应用.要求学生对基本定理和性质熟练记忆.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
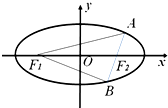 已知F1,F2为椭圆的两个焦点,|F1F2|=6,如图△AF1B的顶点A、B在椭圆上,F2在边AB上,其周长为20,则椭圆的离心率为( )
已知F1,F2为椭圆的两个焦点,|F1F2|=6,如图△AF1B的顶点A、B在椭圆上,F2在边AB上,其周长为20,则椭圆的离心率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
设a=∫
(sinx+cosx)dx,则二项式(a
-
)6展开式中各项系数之和是( )
π 0 |
| x |
| 1 | ||
|
| A、1 | B、-1 | C、2 | D、0 |
 如图,已知多面体ABC-DEFG,三条棱AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.
如图,已知多面体ABC-DEFG,三条棱AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.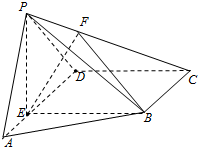 如图,在四棱锥P=ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2
如图,在四棱锥P=ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2