题目内容
甲、乙两人约定晚上6点至晚上7点在某处见面,并约定甲若早到应等乙半小时,乙若早到则不需等甲.若甲、乙两人均在晚上6点至晚上7点之间到达见面地点,求甲、乙两人能见面的概率.
考点:几何概型
专题:概率与统计
分析:由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1},写出满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,y-x|<
或y<x},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
| 1 |
| 2 |
解答:
解:由题意知本题是一个几何概型,设甲到的时间为x,乙到的时间为y,
则试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1},
事件对应的集合表示的面积是s=1,
满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,y-x<
或y<x},
则B(0,
),D(
,1),C(0,1),
则事件A对应的集合表示的面积是
×
×
+
×1×1=
根据几何概型概率公式得到P=
=
,
所以甲、乙两人不能见面的概率P=
=
.能见面的概率是1-
=
,
故答案为:
则试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1},
事件对应的集合表示的面积是s=1,

满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,y-x<
| 1 |
| 2 |
则B(0,
| 1 |
| 2 |
| 1 |
| 2 |
则事件A对应的集合表示的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 8 |
根据几何概型概率公式得到P=
| ||
| 1 |
| 5 |
| 8 |
所以甲、乙两人不能见面的概率P=
| ||
| 1 |
| 5 |
| 8 |
| 5 |
| 8 |
| 3 |
| 8 |
故答案为:
| 3 |
| 8 |
点评:本题主要考查几何概型的概率计算,对于这样的问题,一般要通过把试验发生包含的事件所对应的区域求出,根据集合对应的图形面积,用面积的比值得到结果.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
若直线y=m与y=3x-x3的图象有三个不同的交点,则实数m的取值范围为( )
| A、-2<m<2 |
| B、-2≤m≤2 |
| C、m<-2或m>2 |
| D、m<-2或m≥2 |
 如图,已知多面体ABC-DEFG,三条棱AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.
如图,已知多面体ABC-DEFG,三条棱AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.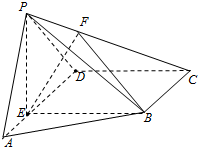 如图,在四棱锥P=ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2
如图,在四棱锥P=ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2