题目内容
设一个焦点为(-1,0),且离心率e=
的椭圆C:
+
=1(a>b>0)上下两顶点分别为A,B,直线y=kx+2交椭圆C于P,Q两点,直线PB与直线y=
交于点M.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求证:A,M,Q三点共线.
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求证:A,M,Q三点共线.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆C的方程.
(Ⅱ)联立
,得(2k2+1)x2+8kx+6=0,由此利用韦达定理、直线方程,结合已知条件能证明A,M,Q三点共线.
|
(Ⅱ)联立
|
解答:
(Ⅰ)解:∵椭圆C:
+
=1(a>b>0)一个焦点为(-1,0),
且离心率e=
,
∴
,解得a=
,c=1,
∴b2=a2-c2=2-1=1,
∴椭圆C的方程为
+y2=1.
(Ⅱ)证明:联立
,得(2k2+1)x2+8kx+6=0,
△=64k2-24(2k2+1)>0,
设P(x1,y1),Q(x2,y2),则x1 +x2=-
,x1x2=
,
∵A(0,1),B(0,-1),
∴直线BP:y+1=
x,直线AQ:y-1=
x ,
∵直线PB与直线y=
交于点M,∴M(
•
,
),
把M(
•
,
)代入直线AQ,得:
-
=
•
•
=
•
=
•
=
•
=
•
=
•
=
•
=-
,成立.
∴A,M,Q三点共线.
| x2 |
| a2 |
| y2 |
| b2 |
且离心率e=
| ||
| 2 |
∴
|
| 2 |
∴b2=a2-c2=2-1=1,
∴椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)证明:联立
|
△=64k2-24(2k2+1)>0,
设P(x1,y1),Q(x2,y2),则x1 +x2=-
| 8k |
| 2k2+1 |
| 6 |
| 2k2+1 |
∵A(0,1),B(0,-1),
∴直线BP:y+1=
| y1+1 |
| x1 |
| y2-1 |
| x2 |
∵直线PB与直线y=
| 1 |
| 2 |
| 3 |
| 2 |
| x1 |
| y1+1 |
| 1 |
| 2 |
把M(
| 3 |
| 2 |
| x1 |
| y1+1 |
| 1 |
| 2 |
-
| 1 |
| 2 |
| y2-1 |
| x2 |
| 3 |
| 2 |
| x1 |
| y1+1 |
=
| 3 |
| 2 |
| x1y2-x1 |
| x2y1+x2 |
=
| 3 |
| 2 |
| x1(kx2+2)-x1 |
| x2(kx1+2)+x2 |
=
| 3 |
| 2 |
| kx1x2+x1 |
| kx1x2+3x2 |
=
| 3 |
| 2 |
| ||
|
=
| 3 |
| 2 |
| 6k+(2k2+1)x1 |
| 6k+(6k2+3)x2 |
=
| 3 |
| 2 |
| -2k-(2k2+1)x2 |
| 6k+(6k2+3)x2 |
=-
| 1 |
| 2 |
∴A,M,Q三点共线.
点评:本题考查椭圆方程的求法,考查三点共线的证明,解题时要认真审题,注意直线方程、韦达定理、椭圆性质等知识点的合理运用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
某考察团对全国10大城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查发现,y与x具有相关关系,回归方程为
=0.66x+1.562.若某城市居民人均消费水平为7.675(千元),估计该城市人均消费额占人均工资收入的百分比约为( )
 |
| y |
| A、83% | B、72% |
| C、67% | D、66% |
用数学归纳法证明1+a+a2+…+an+1=
(a≠1,n∈N*),在验证当n=1时,等式左边应为( )
| 1-an+2 |
| 1-a |
| A、1 |
| B、1+a |
| C、1+a+a2 |
| D、1+a+a2+a3 |
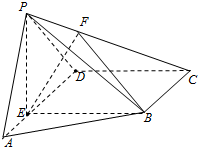 如图,在四棱锥P=ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2
如图,在四棱锥P=ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2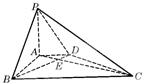 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°PA⊥平面,PA=4,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°PA⊥平面,PA=4,AD=2,AB=2