题目内容
设l,m为两条不同的直线,α为一个平面,下列命题中正确的命题是( )
①若l∥α,m?α,则l∥m;
②若l,m?α,且l∥m,若l∥α,则m∥α;
③若l⊥α,m⊥α,则l∥m;
④若l⊥m,m⊥α,则l∥α.
①若l∥α,m?α,则l∥m;
②若l,m?α,且l∥m,若l∥α,则m∥α;
③若l⊥α,m⊥α,则l∥m;
④若l⊥m,m⊥α,则l∥α.
| A、②③ | B、②④ |
| C、①②③ | D、②③④ |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:画出正方体图形,由正方体中的各条棱之间的关系,举反例说明命题①、④是错误的;
通过空间中的平行与垂直关系判定命题②、③是正确的.
通过空间中的平行与垂直关系判定命题②、③是正确的.
解答:
解:如图所示,正方体ABCD-A1B1C1D1中,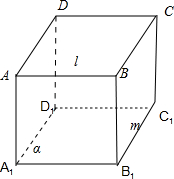 ;
;
对于①,设AB=l,B1C1=m,平面A1B1C1D1=α,满足l∥α,m?α,但l与m不平行,∴命题错误;
对于②,∵l,m?α,且l∥m,当l∥α时,存在n?α,使n∥l,∴n∥m,∴m∥α,命题正确;
对于③,∵l⊥α,m⊥α,根据垂直于同一平面的两条直线互相平行,得出l∥m,∴命题正确;
对于④,结合正方体图形,设A1B1=l,BB1=m,平面A1B1C1D1=α,满足l⊥m,m⊥α,但l与α不平行,∴命题错误.
以上正确的命题是②③;
故选:A.
 ;
;对于①,设AB=l,B1C1=m,平面A1B1C1D1=α,满足l∥α,m?α,但l与m不平行,∴命题错误;
对于②,∵l,m?α,且l∥m,当l∥α时,存在n?α,使n∥l,∴n∥m,∴m∥α,命题正确;
对于③,∵l⊥α,m⊥α,根据垂直于同一平面的两条直线互相平行,得出l∥m,∴命题正确;
对于④,结合正方体图形,设A1B1=l,BB1=m,平面A1B1C1D1=α,满足l⊥m,m⊥α,但l与α不平行,∴命题错误.
以上正确的命题是②③;
故选:A.
点评:本题通过命题真假的判定,考查了空间中的平行与垂直的关系,解题时应结合常见的正方体或长方体模型,以及空间中的平行与垂直关系,对每一个命题进行判定,是综合题.

练习册系列答案
相关题目
任取一个三位正整数N,对数log2N是一个正整数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知全集U={0,1,2,3,4,5,6},集合A={1,2},B={0,2,5},则集合∁U(A∪B)=( )
| A、{0,1,2,5} |
| B、{2} |
| C、{0,1,3,4,5,6} |
| D、{3,4,6} |
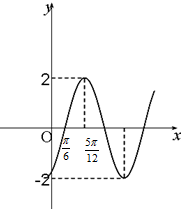 函数f(x)=2sin(ωx+φ),(ω>0,-
函数f(x)=2sin(ωx+φ),(ω>0,-| π |
| 2 |
| π |
| 2 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向右平移
| ||||
D、向右平移
|
若曲线y=x3+ax在坐标原点处的切线方程是2x-y=0,则实数a=( )
| A、1 | B、-1 | C、2 | D、-2 |
等差数列{an}中,a1=7,a3=3,前n项和为Sn,则n=( )时,Sn取到最大值.
| A、4或5 | B、4 | C、3 | D、2 |
在数列{an}中,a1,a2,a3,…,an满足an+1-2an=0,a1>0,则( )
| A、a1+s8-s7>3a4 |
| B、a1+s8-s7<3a4 |
| C、a1+s8-s7=3a4 |
| D、a1+s8-s7与3a4的大小关系不能由已知条件确定 |