题目内容
等差数列{an}中，a1=7，a3=3，前n项和为Sn，则n=（ ）时，Sn取到最大值．
| A、4或5 | B、4 | C、3 | D、2 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由已知条件推导出d=-2，从而得到Sn=-n2+8n，由此利用配方法能求出n=4时，Sn取到最大值．
解答：
解：等差数列{an}中，
∵a1=7，a3=3，∴7+2d=3，解得d=-2，
∴Sn=7n+
×(-2)=-n2+8n=-（n2-8n）=-（n-4）2+16，
∴n=4时，Sn取到最大值．
故选：B．
∵a1=7，a3=3，∴7+2d=3，解得d=-2，
∴Sn=7n+
| n(n-1) |
| 2 |
∴n=4时，Sn取到最大值．
故选：B．
点评：本题考查等差数列的前n项和取得最大值时n的求法，是基础题，解题时要认真审题，注意配方法的合理运用．
练习册系列答案
相关题目
已知中心在坐标原点，焦点在y轴上的双曲线的渐近线方程为y=±
x，则此双曲线的离心率为（ ）
| 1 |
| 2 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
设l，m为两条不同的直线，α为一个平面，下列命题中正确的命题是（ ）
①若l∥α，m?α，则l∥m；
②若l，m?α，且l∥m，若l∥α，则m∥α；
③若l⊥α，m⊥α，则l∥m；
④若l⊥m，m⊥α，则l∥α．
①若l∥α，m?α，则l∥m；
②若l，m?α，且l∥m，若l∥α，则m∥α；
③若l⊥α，m⊥α，则l∥m；
④若l⊥m，m⊥α，则l∥α．
| A、②③ | B、②④ |
| C、①②③ | D、②③④ |
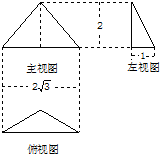已知一个三棱锥的三视图如图所示，其中俯视图是等腰三角形，则该三棱锥的体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知
=（1，-1），
=（λ，1），
与
的夹角为钝角，则λ的取值范围是（ ）
| a |
| b |
| a |
| b |
| A、λ＞1 |
| B、λ＜1 |
| C、λ＜-1 |
| D、λ＜-1或-1＜λ＜1 |
在直三棱柱中，AA1=AB=BC=3，AC=2，D是AC的中点．