题目内容
已知集合A={x|2x2-5x+2≤0},集合B={x|y=log2(ax2-2x+2)}
(Ⅰ)求集合A;
(Ⅱ)若B=R,求实数a的取值范围;
(Ⅲ)若A∩B≠∅,求实数a的取值范围.
(Ⅰ)求集合A;
(Ⅱ)若B=R,求实数a的取值范围;
(Ⅲ)若A∩B≠∅,求实数a的取值范围.
考点:子集与交集、并集运算的转换,对数函数的定义域
专题:函数的性质及应用,集合
分析:(Ⅰ)根据不等式的解法即可求集合A;
(Ⅱ)若B=R,利用对数函数成立的条件,求实数a的取值范围;
(Ⅲ)若A∩B≠∅,得到集合B的取值情况,求实数a的取值范围.
(Ⅱ)若B=R,利用对数函数成立的条件,求实数a的取值范围;
(Ⅲ)若A∩B≠∅,得到集合B的取值情况,求实数a的取值范围.
解答:
解:(Ⅰ)∵A={x|2x2-5x+2≤0}={x|
≤x≤2},
∴A={x|
≤x≤2}.
(Ⅱ)B=R,则ax2-2x+2>0恒成立,
若a=0,则不满足条件,
若a≠0,则
,即a>
,
∴实数a的取值范围是{a|a>
}.
(Ⅲ)若A∩B≠∅,则在[
,2]内,至少有一个值,使ax2-2x+2>0成立,
即在[
,2]内,至少有一个值使a>
+
成立,
设u=-
+
=-2(
-
)2+
则当x∈[
,2]时,u∈[-4,
],
∴a>-4,
即a的取值范围是{a|a>-4}.
| 1 |
| 2 |
∴A={x|
| 1 |
| 2 |
(Ⅱ)B=R,则ax2-2x+2>0恒成立,
若a=0,则不满足条件,
若a≠0,则
|
| 1 |
| 2 |
∴实数a的取值范围是{a|a>
| 1 |
| 2 |
(Ⅲ)若A∩B≠∅,则在[
| 1 |
| 2 |
即在[
| 1 |
| 2 |
| -2 |
| x2 |
| 2 |
| x |
设u=-
| 2 |
| x2 |
| 2 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
则当x∈[
| 1 |
| 2 |
| 1 |
| 2 |
∴a>-4,
即a的取值范围是{a|a>-4}.
点评:本题主要考查集合的基本应用,利用不等式的解法求出集合A,B是解决本题的关键.

练习册系列答案
相关题目
 在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC的中点.
在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC的中点. 如图,已知点P(x0,y0)到直线l:Ax+By+C=0(AB≠0)的距离为d,求证:d=
如图,已知点P(x0,y0)到直线l:Ax+By+C=0(AB≠0)的距离为d,求证:d=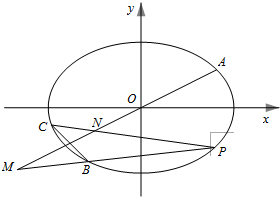 如图,在平面直角坐标系xOy中,已知A,B,C是椭圆
如图,在平面直角坐标系xOy中,已知A,B,C是椭圆