题目内容
已知函数f(x)=x-m
+5,当1≤x≤9时,f(x)>1有恒成立,则实数m的取值范围为( )
| x |
A、m<
| ||
| B、m<5 | ||
| C、m<4 | ||
| D、m≤5 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:令t=
,则由1≤x≤9可得t∈[1,3],由题意可得f(x)=g(t)=t2-mt+5>1在[1,3]上恒成立,即gmin(t)>1.再利用二次函数的性质,分类讨论求得实数m的取值范围.
| x |
解答:
解:令t=
,则由1≤x≤9可得t∈[1,3],
由题意可得f(x)=g(t)=t2-mt+5=(t-
)2+5-
>1在[1,3]上恒成立,
故有gmin(t)>1.
①当
<1时,函数g(t)在[1,3]上单调递增,函数g(t)的最小值为g(1)=6-m,
由6-m>1,求得m<5,综合可得m<2.
②当
∈[1,3]时,函数g(t)在[1,
]上单调递减,在(
3]上单调递增,
函数g(t)的最小值为g(
)=5-
>1,由此求得-4<t<4,综合可得2≤m<4.
③当
>3时,函数g(t)在[1,3]上单调递减,函数g(t)的最小值为g(3)=14-3m,
由14-3m>1,求得m<
,综合可得m无解.
综上可得,m<4.
| x |
由题意可得f(x)=g(t)=t2-mt+5=(t-
| m |
| 2 |
| t2 |
| 4 |
故有gmin(t)>1.
①当
| m |
| 2 |
由6-m>1,求得m<5,综合可得m<2.
②当
| m |
| 2 |
| m |
| 2 |
| m |
| 2 |
函数g(t)的最小值为g(
| m |
| 2 |
| t2 |
| 4 |
③当
| m |
| 2 |
由14-3m>1,求得m<
| 13 |
| 3 |
综上可得,m<4.
点评:本题主要考查二次函数的性质,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
三个数e-
,log0.23,lnπ的大小关系为( )
| 2 |
A、log0.23<e-
| ||
B、log0.23<lnπ<e-
| ||
C、e-
| ||
D、log0.23<lnπ<e-
|
 如图,已知抛物线C:y2=x和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)做两条直线与⊙M相切于A、B两点,分别交抛物线于E、F两点.
如图,已知抛物线C:y2=x和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)做两条直线与⊙M相切于A、B两点,分别交抛物线于E、F两点.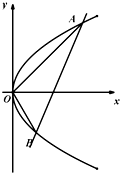 如图,已知抛物线y2=2px(p>0)上点(2,a)到焦点F的距离为3,直线l:my=x+t(t≠0)交抛物线C于A,B两点,且满足OA⊥OB.圆E是以(-p,p)为圆心,p为直径的圆.
如图,已知抛物线y2=2px(p>0)上点(2,a)到焦点F的距离为3,直线l:my=x+t(t≠0)交抛物线C于A,B两点,且满足OA⊥OB.圆E是以(-p,p)为圆心,p为直径的圆.