题目内容
(1)已知|2x-3|≤1的解集为[m,n]
①求m+n的值;
②若|x-a|<m,求证:|x|<|a|+1.
(2)已知x,y,z为正实数,且
+
+
=1,求x+4y+9z的最小值及取得最小值时x,y,z的值.
①求m+n的值;
②若|x-a|<m,求证:|x|<|a|+1.
(2)已知x,y,z为正实数,且
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
考点:平均值不等式在函数极值中的应用
专题:计算题,不等式
分析:(1)①由不等式|2x-3|≤1可得1≤x≤2,则m=1,n=2;
②化|x|=|x-a+a|≤|x-a|+|a|,从而证明;
(2)利用柯西不等式求最小值即取最小值的条件.
②化|x|=|x-a+a|≤|x-a|+|a|,从而证明;
(2)利用柯西不等式求最小值即取最小值的条件.
解答:
解:(1)①由不等式|2x-3|≤1可化为-1≤2x-3≤1得1≤x≤2,
∴m=1,n=2,
∴m+n=3;
②证明:∵|x-a|<1,
∴|x|=|x-a+a|≤|x-a|+|a|<|a|+1.
(3)解:由柯西不等式得
当且仅当x=2y=3z,即x=6,y=3,z=2时,等号成立;
所以当x=6,y=3,z=2时,x+4y+9z取得最小值36.
∴m=1,n=2,
∴m+n=3;
②证明:∵|x-a|<1,
∴|x|=|x-a+a|≤|x-a|+|a|<|a|+1.
(3)解:由柯西不等式得
|
当且仅当x=2y=3z,即x=6,y=3,z=2时,等号成立;
所以当x=6,y=3,z=2时,x+4y+9z取得最小值36.
点评:本题考查了绝对值不等式的解法及证明,同时考查了柯西不等式在求最值时的应用,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=3x+x,g(x)=log3x+2,h(x)=log3x+x的零点依次是a,b,c,则a,b,c,的大小关系是( )
| A、a<b<c |
| B、a<c<b |
| C、c<b<a |
| D、b<a<c |
已知函数f(x)=x-m
+5,当1≤x≤9时,f(x)>1有恒成立,则实数m的取值范围为( )
| x |
A、m<
| ||
| B、m<5 | ||
| C、m<4 | ||
| D、m≤5 |
设函数f(x)=lnx-ax+2.
(1)若a>0,求函数f(x)的单调区间和极值;
(2)若a>-e时,函数g(x)=ex-xf′(x)在[
,3]上有最大值e3,其中f′(x)的导数,求实数a的值.
(1)若a>0,求函数f(x)的单调区间和极值;
(2)若a>-e时,函数g(x)=ex-xf′(x)在[
| 1 |
| 2 |
在长方体ABCD-A1B1C1D1中,AB=
,B1B=BC=1,则线BC1与面BDD1B1所成角的正弦为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
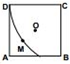
 如图,△ADP为正三角形,O为正方形ABCD中心,而ADP⊥面ABCD,M为面ABCD内的点,且满足MP=MC.则点M在正方形ABCD内的轨迹为( )
如图,△ADP为正三角形,O为正方形ABCD中心,而ADP⊥面ABCD,M为面ABCD内的点,且满足MP=MC.则点M在正方形ABCD内的轨迹为( )