题目内容
三个数e-
,log0.23,lnπ的大小关系为( )
| 2 |
A、log0.23<e-
| ||
B、log0.23<lnπ<e-
| ||
C、e-
| ||
D、log0.23<lnπ<e-
|
考点:对数值大小的比较
专题:函数的性质及应用
分析:根据指数函数,对数函数和幂函数的性质求出a,b,c的取值范围即可确定中间的数.
解答:
解:∵0<e-
<1,log0.23<0,lnπ>1,
故log0.23<e-
<lnπ.
故选:A.
| 2 |
故log0.23<e-
| 2 |
故选:A.
点评:本题主要考查函数值的大小比较,利用指数函数,对数函数和幂函数的性质确定a,b,c的取值范围是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=3x+x,g(x)=log3x+2,h(x)=log3x+x的零点依次是a,b,c,则a,b,c,的大小关系是( )
| A、a<b<c |
| B、a<c<b |
| C、c<b<a |
| D、b<a<c |
已知集合A={0,1,2},B{1,2,3},则∁(A∪B)(A∩B)=( )
| A、{0,3} |
| B、{1,2} |
| C、∅ |
| D、{0,1,2,3} |
已知函数f(x)=x-m
+5,当1≤x≤9时,f(x)>1有恒成立,则实数m的取值范围为( )
| x |
A、m<
| ||
| B、m<5 | ||
| C、m<4 | ||
| D、m≤5 |
在长方体ABCD-A1B1C1D1中,AB=
,B1B=BC=1,则线BC1与面BDD1B1所成角的正弦为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
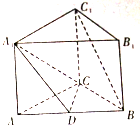 如图,直三棱柱ABC-A
如图,直三棱柱ABC-A