题目内容
已知数列{an}的首项为1,对任意的n∈N*,定义bn=an+1-an.
(Ⅰ) 若bn=n+1
(i)求a3的值和数列{an}的通项公式;
(ii)求数列{
}的前n项和Sn;
(Ⅱ)若bn+1=bn+2bn(n∈N*),且b1=2,b2=3,求数列{bn}的前3n项的和.
(Ⅰ) 若bn=n+1
(i)求a3的值和数列{an}的通项公式;
(ii)求数列{
| 1 |
| an |
(Ⅱ)若bn+1=bn+2bn(n∈N*),且b1=2,b2=3,求数列{bn}的前3n项的和.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)(i)由a1=1,a2=a1+b1,可得a3=a2+b2.
由an+1-an=n+1可得当n≥2时,an=a1+(a2-a1)+…+(an-an-1),再利用等差数列的前n项和公式即可得出.
(ii)由(i)得:
=
=2(
-
),利用“裂项求和”即可得出.
(II)对任意的n∈N*有bn+1=bn+2bn(n∈N*),且b1=2,b2=3,可得bn+6=
=
=
=
=bn,即数列{bn}各项的值重复出现,周期为6.对n分类讨论即可得出.
由an+1-an=n+1可得当n≥2时,an=a1+(a2-a1)+…+(an-an-1),再利用等差数列的前n项和公式即可得出.
(ii)由(i)得:
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(II)对任意的n∈N*有bn+1=bn+2bn(n∈N*),且b1=2,b2=3,可得bn+6=
| bn+5 |
| bn+4 |
| bn+4 |
| bn+3bn+4 |
| 1 |
| bn+3 |
| bn+1 |
| bn+2 |
解答:
解:(Ⅰ)(i)∵a1=1,a2=a1+b1=1+2=3,
∴a3=a2+b2=3+3=6.
.由an+1-an=n+1得
当n≥2时,an=a1+(a2-a1)+…+(an-an-1)
=1+2+…+n
=
,
而a1=1适合上式,
∴an=
.
(ii)由(i)得:
=
=2(
-
),
∴Sn=
+
+
+…+
=2[(1-
)+(
-
)+…+(
-
)]
=2(1-
)
=
.
(Ⅱ)∵对任意的n∈N*有bn+1=bn+2bn(n∈N*),且b1=2,b2=3,
∴bn+6=
=
=
=
=bn,
∴数列{bn}各项的值重复出现,周期为6.
又数列{bn}的前6项分别为2,3,
,
,
,
,且这六个数的和为8.
设数列{bn}的前n项和为Sn,则,
当n=2k(k∈N*)时,
S3n=S6k=k(b1+b2+…+b6)=8k,
当n=2k+1(k∈N*)时,
S3n=S6k+3=k(b1+b2+…+b6)+b1+b2+b3=8k+
,
当n=1时,S3=
.
∴当n为偶数时,S3n=4n;当n为奇数时,S3n=4n+
.
∴a3=a2+b2=3+3=6.
.由an+1-an=n+1得
当n≥2时,an=a1+(a2-a1)+…+(an-an-1)
=1+2+…+n
=
| n(n+1) |
| 2 |
而a1=1适合上式,
∴an=
| n(n+1) |
| 2 |
(ii)由(i)得:
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=2(1-
| 1 |
| n+1 |
=
| 2n |
| n+1 |
(Ⅱ)∵对任意的n∈N*有bn+1=bn+2bn(n∈N*),且b1=2,b2=3,
∴bn+6=
| bn+5 |
| bn+4 |
| bn+4 |
| bn+3bn+4 |
| 1 |
| bn+3 |
| bn+1 |
| bn+2 |
∴数列{bn}各项的值重复出现,周期为6.
又数列{bn}的前6项分别为2,3,
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
设数列{bn}的前n项和为Sn,则,
当n=2k(k∈N*)时,
S3n=S6k=k(b1+b2+…+b6)=8k,
当n=2k+1(k∈N*)时,
S3n=S6k+3=k(b1+b2+…+b6)+b1+b2+b3=8k+
| 13 |
| 2 |
当n=1时,S3=
| 13 |
| 2 |
∴当n为偶数时,S3n=4n;当n为奇数时,S3n=4n+
| 5 |
| 2 |
点评:本题考查了等差数列的前n项和公式、“裂项求和”方法、数列的周期性;考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知函数f(x)=x
(x>0),若对于任意α∈(0,
),都有f(tanα)+f(
)≥4cosβ(0≤β≤2π)成立,则β的取值范围是( )
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| tanα |
A、[
| ||||
B、[
| ||||
C、[0,
| ||||
D、[0,
|
函数y=ex+m(其中e是自然对数的底数)的图象上存在点(x,y)满足条件:
则实数m的取值范围是( )
|
| A、[-1,2e-e2] |
| B、[2-e2,-1] |
| C、[2-e2,2e-e2] |
| D、[2-e2,0] |
已知条件p:log2(x-1)<1;条件q:|x-2|<1|,则p是q成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
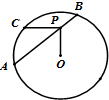 如图,AB是圆O的一条弦,点P是AB上一点,点C是圆O上一点,PC⊥OP,AP=4,PB=2,则PC=
如图,AB是圆O的一条弦,点P是AB上一点,点C是圆O上一点,PC⊥OP,AP=4,PB=2,则PC=