题目内容
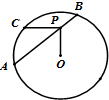如图，AB是圆O的一条弦，点P是AB上一点，点C是圆O上一点，PC⊥OP，AP=4，PB=2，则PC=考点：与圆有关的比例线段
专题：立体几何
分析：延长CP，交圆O于D，由垂径定理得CP=PD，由相交弦定理，得AP•PB=CP•PD，由此能求出PC．
解答：
解：延长CP，交圆O于D，
∵AB是圆O的一条弦，点P是AB上一点，点C是圆O上一点，PC⊥OP，AP=4，PB=2，
∴PC=PD，
由相交弦定理，得：
AP•PB=PC•PD，
∴PC2=4×2=8，
∴PC=2
．
故答案为：2
．
∵AB是圆O的一条弦，点P是AB上一点，点C是圆O上一点，PC⊥OP，AP=4，PB=2，
∴PC=PD，
由相交弦定理，得：
AP•PB=PC•PD，
∴PC2=4×2=8，
∴PC=2
| 2 |
故答案为：2
| 2 |
点评：本题考查线段长的求法，是中档题，解题时要注意垂径定理和相交弦定理的合理运用．
练习册系列答案
相关题目
为了解某校高三学生的视力情况，随机抽查了该校50名高三学生，得到如图所示的频率分布直方图．若α、β均为锐角，且2sinα=sinαcosβ+cosαsinβ，则α与β的大小关系为（ ）
| A、α＜β | B、α＞β |
| C、α≤β | D、不确定 |
执行如图的程序框图，输入x=-2，h=1，那么输出的各个数的和等于（ ）
| A、0 | B、1 | C、2 | D、3 |
如果执行如图的程序框图，那么输出的S为 （ ）
| A、S=2 | ||
B、S=-
| ||
| C、S=-3 | ||
D、S=
|
设x∈R，则“x2＞1”是“x2＞x”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |