题目内容
已知椭圆
+
=1(a>b>0)的焦点分别是F1、F2,上顶点为B2,若△F1 B2F2是等边三角形,则椭圆的离心率e= .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用椭圆的性质得出|F1F2|=2c,|B2F1|=a,利用△F1B2F2为等边三角形,求出椭圆的离心率e.
解答:
解:根据题意,画出图形,如图所示;

在椭圆
+
=1(a>b>0)中,
∵|F1F2|=2c,
|B2F1|=
=
=a,
且△F1B2F2为等边三角形,
∴|B2F1|=|F1F2|=2c,
∴椭圆的离心率为e=
=
.
故答案为:
.

在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∵|F1F2|=2c,
|B2F1|=
| OF12+OB22 |
| c2+b2 |
且△F1B2F2为等边三角形,
∴|B2F1|=|F1F2|=2c,
∴椭圆的离心率为e=
| c |
| a |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了椭圆的几何性质的应用问题,解题时应画出图形,结合图形进行解答,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知定义在R上的函数f(x)满足f[f(x)]=xf(x)+1,则方程f(x)=0的实根个数为( )
| A、0 | B、1 | C、2 | D、4 |
已知偶函数y=f(x)在区间[0,+∞)为增函数,则f(-3)和f(π)大小关系是( )
| A、f(-3)>f(π) |
| B、f(-3)<f(π) |
| C、f(-3)=f(π) |
| D、不能确定 |
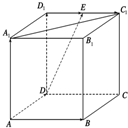 如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.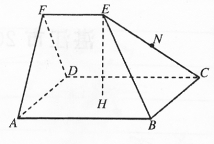 如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.
如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.