Question

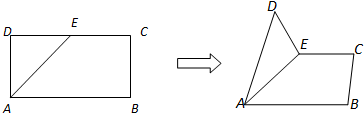
如图，在矩形ABCD中，AB=4，BC=2，E为DC边的中点，沿AE将△ADE折起，使二面角D-AE-B为90°，则直线BD与面ABCE所成角的正弦值为

 

．

Answer 1

考点：直线与平面所成的角

专题：计算题,空间位置关系与距离,空间角

分析：作DO⊥AE，垂足为O，由于二面角D-AE-B为90°，则DO⊥平面ABCE，连接BO，则∠DBO为直线BD和平面ABCE所成的角，解三角形OBD，即可求出直线BD与面ABCE所成角的正弦值．

解答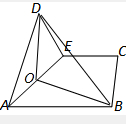： 解：作DO⊥AE，垂足为O，
由于二面角D-AE-B为90°，则DO⊥平面ABCE，
连接BO，则∠DBO为直线BD和平面ABCE所成的角，
在三角形ADE中，AD=DE=2，AE=2

2

，则DO=

2

，
在三角形ABO中，AB=4，AO=

2

，∠BAE=45°，
则BO=

2+16-2 2 ×4× 2 2

=

10

，
即有DB=

10+2

=2

3

，
则sin∠DBO=

2

2 3

=

6

6

．
故答案为：

6

6

．

点评：本题考查的知识点是直线与平面所成的角，其中添加辅助线，构造出∠OBD为直线BD与面ABCE所成角，将线面夹角问题转化为解三角形问题，是解答本题的关键．