题目内容
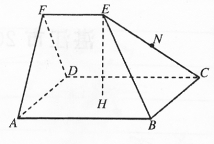 如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.
如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.(1)证明:EH∥平面ADF;
(2)证明:平面ADF丄平面ABCD;
(3)求五面体EF-ABCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知得EF∥AB且EF=
AB,取AD的中点G,连结GH,GF,证明FG∥EH,利用直线与平面平行的判定定理证明EH∥平面ADF.
(2)证明FG⊥平面ABCD,利用直线与平面垂直的判定定理证明平面ADF⊥平面ABCD.
(2)说明GH为该柱体的高,利用VABCD-EF=VADF-RTE+VE-BCTR求解即可.
| 1 |
| 2 |
(2)证明FG⊥平面ABCD,利用直线与平面垂直的判定定理证明平面ADF⊥平面ABCD.
(2)说明GH为该柱体的高,利用VABCD-EF=VADF-RTE+VE-BCTR求解即可.
解答:
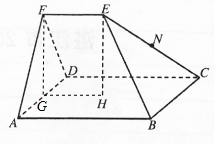 证明:(1)由已知得EF∥AB且EF=
证明:(1)由已知得EF∥AB且EF=
AB
取AD的中点G,连结GH,GF…..(1分)
则GH∥AB且GH=
AB…(2分)
EF∥GH且EF=GH,即EFGH为平行四边形
∴FG∥EH,FG?平面ADF,EH?平面ADF
∴EH∥平面ADF;
(2)∵EH⊥平面ABCD,且FG∥EH,…(7分)
∴FG⊥平面ABCD,且FG?平面ADF,…(9分)
∴平面ADF⊥平面ABCD;….(10分)
(2)解:在面ABCD内过H作RT∥AD,
如图,则面RTE∥面ADF,ADF-RTE为三棱柱,
由(1)及HG⊥AD得GH为该柱体的高,….(12分)
∴VABCD-EF=VADF-RTE+VE-BCTR
=(
×2×1)×1+
×(2×1)×1=
.(不排除其它方法,酌情分布给分)
 证明:(1)由已知得EF∥AB且EF=
证明:(1)由已知得EF∥AB且EF=| 1 |
| 2 |
取AD的中点G,连结GH,GF…..(1分)
则GH∥AB且GH=
| 1 |
| 2 |
EF∥GH且EF=GH,即EFGH为平行四边形
∴FG∥EH,FG?平面ADF,EH?平面ADF
∴EH∥平面ADF;
(2)∵EH⊥平面ABCD,且FG∥EH,…(7分)
∴FG⊥平面ABCD,且FG?平面ADF,…(9分)
∴平面ADF⊥平面ABCD;….(10分)
(2)解:在面ABCD内过H作RT∥AD,
如图,则面RTE∥面ADF,ADF-RTE为三棱柱,
由(1)及HG⊥AD得GH为该柱体的高,….(12分)
∴VABCD-EF=VADF-RTE+VE-BCTR
=(
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 3 |
点评:本题考查直线与平面平行的判定定理以及平面与平面垂直的判定定理,几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
已知△ABC的内角A,B,C的对边分别为a,b,c,若csinC=acosB+bcosA,则△ABC的形状为( )
| A、锐角三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、钝角三角形 |