题目内容
已知偶函数y=f(x)在区间[0,+∞)为增函数,则f(-3)和f(π)大小关系是( )
| A、f(-3)>f(π) |
| B、f(-3)<f(π) |
| C、f(-3)=f(π) |
| D、不能确定 |
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:由偶函数得f(-3)=f(3),由于f(x)在区间[0,+∞)为增函数,则由3<π,即可比较大小.
解答:
解:偶函数y=f(x)有f(-x)=f(x),
则f(-3)=f(3),
由于f(x)在区间[0,+∞)为增函数,
则由3<π,即有f(3)<f(π),
即f(-3)<f(π).
故选B.
则f(-3)=f(3),
由于f(x)在区间[0,+∞)为增函数,
则由3<π,即有f(3)<f(π),
即f(-3)<f(π).
故选B.
点评:本题考查函数的奇偶性和单调性的运用:比较大小,注意转化的思想方法,同时注意函数的单调区间,属于基础题.

练习册系列答案
相关题目
已知△ABC的内角A,B,C的对边分别为a,b,c,若csinC=acosB+bcosA,则△ABC的形状为( )
| A、锐角三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、钝角三角形 |
下列四条直线中,哪一条是双曲线x2-
=1的渐近线?( )
| y2 |
| 4 |
A、y=-
| ||
B、y=-
| ||
| C、y=2x | ||
| D、y=4x |
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得几何体的体积是( )cm3.
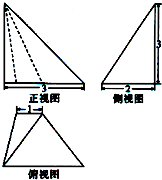

| A、4 | B、3 | C、6 | D、5 |