题目内容
9.某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,每辆车一年内需要维修的人工费用为200元,汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况,整理得下表:| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 40 | 40 |
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:
| 价格(万元) | 25 | 23.5 | 22 | 20.5 |
| 销售量(辆) | 30 | 33 | 36 | 39 |
分析 (1)100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访,A、B、C型汽车各2,4,4辆.从参加问卷到访的10辆汽车中随机抽取两辆,有${C}_{10}^{2}$=45种方法,即可求这两辆汽车来自同一类型的概率;
(2)ξ的取值为0,200,400,600,求出相应的概率,即可求ξ的分布列及数学期望;
(3)求出b,即可预测月销售量.
解答 解:(1)100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访,A、B、C型汽车各2,4,4辆.
从参加问卷到访的10辆汽车中随机抽取两辆,有${C}_{10}^{2}$=45种方法,这两辆汽车来自同一类型的概率为$\frac{{C}_{2}^{2}+2{C}_{4}^{2}}{45}$=$\frac{13}{45}$;
(2)ξ的取值为0,200,400,600,
P(ξ=0)=0.8×0.6×0.6=0.288,P(ξ=200)=0.2×0.6×0.6+0.8×0.4×0.6+0.8×0.6×0.4=0.456,
P(ξ=400)=0.2×0.4×0.6+0.2×0.6×0.4+0.8×0.4×0.4=0.224,
P(ξ=600)=0.2×0.4×0.4=0.032,
∴ξ的分布列
| ξ | 0 | 200 | 400 | 600 |
| P | 0.288 | 0.456 | 0.224 | 0.032 |
(3)$\overline{x}$=$\frac{1}{4}$(25+23.5+22+20.5)=22.75,$\overline{y}$=$\frac{1}{4}$(30+33+36+39)=35.25,
∵$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+80,
∴35.25=$\stackrel{∧}{b}$×22.75+80,
∴$\stackrel{∧}{b}$=$\frac{179}{91}$,
x=19,y=19×$\frac{179}{91}$+80≈117.
点评 本题考查概率的计算,考查分布列及数学期望,考查线性回归方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.某种产品的广告费用支出x(千元)与销售额y(万元)之间有如下对应数据:
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}},\hat a=\bar y-\hat b\bar x$)
(1)根据上表数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程;
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
(2)当广告费用支出10千元时,预测一下该商品的销售额为多少万元?
| x | 2 | 4 | 5 | 6 | 8 |
| y | 3 | 4 | 6 | 5 | 7 |
(1)根据上表数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程;
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
(2)当广告费用支出10千元时,预测一下该商品的销售额为多少万元?
4.在平行四边形ABCD中,对角线AC与BD交于点O,$\overrightarrow{CO}=λ({\overrightarrow{AB}+\overrightarrow{AD}})$,则实数λ=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
1.有分别写着数字1到120的120张卡片,从中取出1张,这样卡片上的数字是2的倍数或是3的倍数的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{2}{3}$ |
18.给出下列命题中正确的是( )
| A. | 棱柱被平面分成的两部分可以都是棱柱 | |
| B. | 底面是矩形的平行六面体是长方体 | |
| C. | 棱柱的底面一定是平行四边形 | |
| D. | 棱锥的底面一定是三角形 |
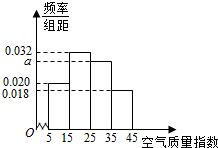 进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.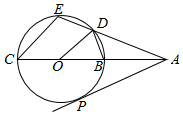 如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,
如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,