题目内容
20.某种产品的广告费用支出x(千元)与销售额y(万元)之间有如下对应数据:| x | 2 | 4 | 5 | 6 | 8 |
| y | 3 | 4 | 6 | 5 | 7 |
(1)根据上表数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程;
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
(2)当广告费用支出10千元时,预测一下该商品的销售额为多少万元?
分析 (1)代入公式求出$\stackrel{∧}{a}$,$\stackrel{∧}{b}$,写出线性回归方程;
(2)将x=10代入回归方程求出销售额的估计值.
解答 解:$\overline{x}$=$\frac{2+4+5+6+8}{5}$=5,$\overline{y}$=$\frac{3+4+6+5+7}{5}$=5,$\stackrel{∧}{b}$=$\frac{138-5×5×5}{145-5×{5}^{2}}$=$\frac{13}{20}$,$\stackrel{∧}{a}$=5-$\frac{13}{20}×5$=$\frac{7}{4}$.
∴销售额y关于费用支出x的线性回归方程是y=$\frac{13}{20}$x+$\frac{7}{4}$.
(2)将x=10,代入(1)中的回归方程,得y=$\frac{13}{20}$×10+$\frac{7}{4}$=$\frac{33}{4}$=8.25.
∴当广告费用支出10千元时,该商品的销售额约为8.25万元.
点评 本题考查了线性回归方程的求解及数据估值,属于基础题.

练习册系列答案
相关题目
15.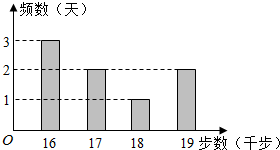 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
(Ⅰ)求小王这8天“健步走”步数的平均数;
(Ⅱ)从步数为16千步,17千步,18千步的几天中任选2天,设小王这2天通过健步走消耗的“能量和”为X,求X的分布列.
 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).| 健步走步数(千卡) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅱ)从步数为16千步,17千步,18千步的几天中任选2天,设小王这2天通过健步走消耗的“能量和”为X,求X的分布列.
9.某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,每辆车一年内需要维修的人工费用为200元,汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况,整理得下表:
假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访.
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:
已知A型汽车的购买量y与价格x符合如下线性回归方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 40 | 40 |
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:
| 价格(万元) | 25 | 23.5 | 22 | 20.5 |
| 销售量(辆) | 30 | 33 | 36 | 39 |
10.数列$1,-\frac{3}{4},\frac{1}{2},-\frac{5}{16},…$的一个通项公式为( )
| A. | ${(-1)^n}\frac{n+1}{2n}$ | B. | ${(-1)^{n+1}}\frac{2n-1}{2n}$ | C. | ${(-1)^{n+1}}\frac{n+1}{2^n}$ | D. | ${(-1)^{n+1}}\frac{2n-1}{2^n}$ |