题目内容
4.在平行四边形ABCD中,对角线AC与BD交于点O,$\overrightarrow{CO}=λ({\overrightarrow{AB}+\overrightarrow{AD}})$,则实数λ=( )| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
分析 可画出图形,根据向量加法的平行四边形法则便可得到$\overrightarrow{CO}=\frac{1}{2}(\overrightarrow{CD}+\overrightarrow{CB})$,由相反向量的概念和向量的数乘运算便可得到$\overrightarrow{CO}=-\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD})$,这便可得到$λ=-\frac{1}{2}$.
解答 解:如图,
$\overrightarrow{CO}=\frac{1}{2}(\overrightarrow{CD}+\overrightarrow{CB})$=$\frac{1}{2}(-\overrightarrow{AB}-\overrightarrow{AD})$=$-\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AD})$;
又$\overrightarrow{CO}=λ(\overrightarrow{AB}+\overrightarrow{AD})$;
∴$λ=-\frac{1}{2}$.
故选:A.
点评 考查向量加法的平行四边形法则,向量的数乘运算,以及相反向量的概念.

练习册系列答案
相关题目
15.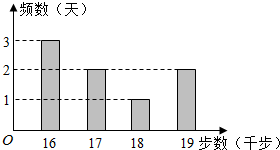 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
(Ⅰ)求小王这8天“健步走”步数的平均数;
(Ⅱ)从步数为16千步,17千步,18千步的几天中任选2天,设小王这2天通过健步走消耗的“能量和”为X,求X的分布列.
 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(如图)及相应的消耗能量数据表(如表).| 健步走步数(千卡) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅱ)从步数为16千步,17千步,18千步的几天中任选2天,设小王这2天通过健步走消耗的“能量和”为X,求X的分布列.
9.某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,每辆车一年内需要维修的人工费用为200元,汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况,整理得下表:
假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访.
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:
已知A型汽车的购买量y与价格x符合如下线性回归方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 40 | 40 |
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:
| 价格(万元) | 25 | 23.5 | 22 | 20.5 |
| 销售量(辆) | 30 | 33 | 36 | 39 |
13.函数$f(x)={log_a}({a{x^2}-x})({0<a<1})$,则该函数的单调减区间为( )
| A. | (-∞,0) | B. | $({-∞,\frac{1}{2a}})$ | C. | $({0,\frac{1}{a}})$ | D. | $({\frac{1}{a},+∞})$ |
14.已知$tanα=\frac{1}{3}$,则$\frac{{{{cos}^2}α-2{{sin}^2}α}}{{{{cos}^2}α}}$=( )
| A. | $\frac{7}{9}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $-\frac{7}{9}$ |
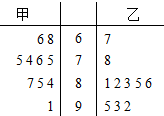 某次歌手大赛中,有10名评委.茎叶图(如图所示)是10名评委给甲、乙两位选手评定的成绩,则选手甲成绩的众数是75,选手乙的中位数是84.
某次歌手大赛中,有10名评委.茎叶图(如图所示)是10名评委给甲、乙两位选手评定的成绩,则选手甲成绩的众数是75,选手乙的中位数是84.