题目内容
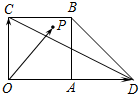 如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设| OP |
| OC |
| OD |
考点:简单线性规划,平面向量的基本定理及其意义
专题:平面向量及应用
分析:因为是正方形,所以可考虑建立平面直角坐标系:以O为原点,OA,OC所在直线分别为x轴,y轴建立平面直角坐标系,这时候可求出
=(0,1),
=(2,0),所以设P(x,y),所以根据已知条件可得:(x,y)=(2β,α),所以可用x,y表示α,β,并得到α+β=
x+y,这样求
x+y的最大值即可.而x,y的取值范围便是△BCD上及其内部,所以可想着用线性规划的知识求解.所以设z=
x+y,y=-
x+z,所以z表示直线y=-
x+z在y轴上的截距,要求α+β的最大值,只需求截距z的最大值即可,而通过图形可看出当该直线过B点时截距最大,所以将B点坐标带入直线方程,即可得到z的最大值,即α+β的最大值.
| OC |
| OD |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:分别以边OA,OC所在直线为x,y轴建立如图所实施平面直角坐标系;
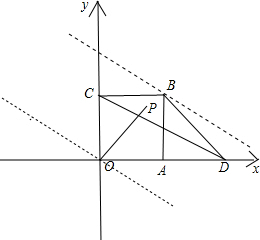 则:
则:
=(0,1),
=(2,0),设P(x,y),
=(x,y);
∴(x,y)=α(0,1)+β(2,0)=(2β,α);
∴
;
∴α+β=
x+y;
设z=
x+y,则:y=-
x+z,所以z是直线y=-
x+z在y轴上的截距;
由图形可以看出,当该直线经过B(1,1)点时,它在y轴的截距z最大,最大为
;
∴α+β的最大值是
.
故答案为:
.
 则:
则:| OC |
| OD |
| OP |
∴(x,y)=α(0,1)+β(2,0)=(2β,α);
∴
|
∴α+β=
| 1 |
| 2 |
设z=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由图形可以看出,当该直线经过B(1,1)点时,它在y轴的截距z最大,最大为
| 3 |
| 2 |
∴α+β的最大值是
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:考查通过建立平面直角坐标系,用向量坐标解决向量问题的方法,利用线性规划求最值的方法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
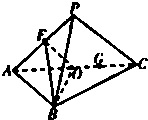 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,O分别为PA,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,O分别为PA,AC的中点,AC=16,PA=PC=10.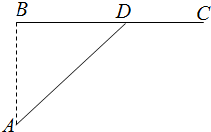 如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ