题目内容
已知椭圆的中心在原点,焦点与双曲线
-
=1的焦点相同,且经过点M(4,1);直线l:y=x+m交椭圆于A、B两点.
(1)求椭圆方程;
(2)若直线l不过点M,试问直线AM,BN与x轴是否能构成一个等腰三角形?请说明理由.
| x2 |
| 10 |
| y2 |
| 5 |
(1)求椭圆方程;
(2)若直线l不过点M,试问直线AM,BN与x轴是否能构成一个等腰三角形?请说明理由.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:向量与圆锥曲线,圆锥曲线的定义、性质与方程
分析:(1)椭圆方程为
+
=1(λ>0),待定系数法求解,(2)解方程组
,得5x2+8mx+4m2-20=0,利用韦达定理求解,k1+k2=
=0即可证明.
| x2 |
| 15+λ |
| y2 |
| λ |
|
| (y1-1)(x2-4)+(x1-4)(y2-1) |
| (x1-4)(x2-4) |
解答:
解:(1)以题意可知,椭圆中的半焦距c2=10+5=15,
设椭圆方程为
+
=1(λ>0)
∵过点M(4,1),
∴
+
=1,∴λ=5或λ=-3(舍去)
∴
+
=1
(2)设A(x1,y1),B(x2,y2),
解方程组
,得5x2+8mx+4m2-20=0
x1+x2=-
,x1x2=
设直线MA.MB的斜率分别为k1,k2,
则k1=
,k2=
,k1+k2=
∵(y1-1)(x2-4)+(y2-1)(x1-4)=2x1x2+(m-5)(x1+x2)-8(m-1)=0,
∴k1+k2=0,
∴直线AM,BN与x轴能构成一个等腰三角形
设椭圆方程为
| x2 |
| 15+λ |
| y2 |
| λ |
∵过点M(4,1),
∴
| 16 |
| 16+λ |
| 1 |
| λ |
∴
| x2 |
| 20 |
| y2 |
| 5 |
(2)设A(x1,y1),B(x2,y2),
解方程组
|
x1+x2=-
| 8m |
| 5 |
| 4m2-20 |
| 5 |
设直线MA.MB的斜率分别为k1,k2,
则k1=
| y1-1 |
| x1-4 |
| y2-1 |
| x2-4 |
| (y1-1)(x2-4)+(x1-4)(y2-1) |
| (x1-4)(x2-4) |
∵(y1-1)(x2-4)+(y2-1)(x1-4)=2x1x2+(m-5)(x1+x2)-8(m-1)=0,
∴k1+k2=0,
∴直线AM,BN与x轴能构成一个等腰三角形
点评:本考查了直线与椭圆的位置关系,结合方程求解,运用韦达定理判断,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
如图:正方体ABCD-A1B1C1D1中,AB1与C1B所成的角为( )
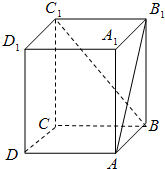

A、
| ||
B、
| ||
C、
| ||
D、
|
某中学拟安排6名实习老师到高一年级的3个班实习,每班2人,则甲在一班、乙不在一班的不同分配方案共有( )
| A、12种 | B、24种 |
| C、36种 | D、48种 |
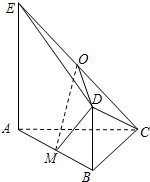 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=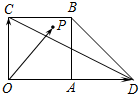 如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设