题目内容
求值：（1）sin105°； （2）cos15°．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由条件应用诱导公式、半角公式化简三角函数式，可得结果．
解答：
解：：（1）sin105°=sin（90°+15°）=cos15°=
=
=
=
；
（2）cos15°=
=
=
=
．
|
|
| ||||
| 2 |
| ||||
| 4 |
（2）cos15°=
|
|
| ||||
| 2 |
| ||||
| 4 |
点评：本题主要考查应用诱导公式、半角公式化简三角函数式，属于基础题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
下列四个命题中，错误的是（ ）
A、已知函数f（x）=
| ||
B、设回归直线方程为
| ||
| C、已知ξ服从正态分布 N（0，σ2），且P（-2≤ξ≤0）=0.4，则P（ξ＞2）=0.1 | ||
| D、对于命题p：“?x∈R，x2+x+1＜0”，则?p：“?x∈R，x2+x+1＞0” |
△ABC中，下面四个等式中不正确的是（ ）
| A、cos（A+B）=-cosC | ||||
| B、sin2（A+B）=sin2C | ||||
C、tan
| ||||
D、cos3（A+B）=1-2cos2
|
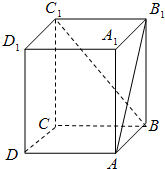
如图：正方体ABCD-A1B1C1D1中，AB1与C1B所成的角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
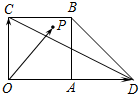如图，四边形OABC是边长为1的正方形，点D在OA的延长线上，且OD=2，点P为△BCD内（含边界）的动点，设