题目内容
设集合I={1,2,3,…,n} (n∈N,n≥2),构造I的两个非空子集A,B,使得B中最小的数大于A中最大的数,则这样的构造方法共有 种.
考点:排列、组合及简单计数问题
专题:计算题,排列组合
分析:由题意得:a1=0,a2=
=1,当n≥2时,an=
+2
+3
+…+(n-1)
,由此能求出an=n2n-1-2n+1(n∈N+).
| C | 2 2 |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
解答:
解:记不同的选择方法种数为an,由题意得:a1=0,a2=
=1
当n≥2时,an=
+2
+3
+…+(n-1)
=(2
+3
+4
+…+n
)-(
+
+
+…+
)
=n2n-1-(2n-1)=n2n-1-2n+1
又a1=0,a2=1也满足,
故an=n2n-1-2n+1.
故答案为:n2n-1-2n+1.
| C | 2 2 |
当n≥2时,an=
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
=(2
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
=n2n-1-(2n-1)=n2n-1-2n+1
又a1=0,a2=1也满足,
故an=n2n-1-2n+1.
故答案为:n2n-1-2n+1.
点评:本题考查排列、组合及简单计数问题,考查数列的通项公式和前n项和公式的求法,是中档题.

练习册系列答案
相关题目
下列四个命题中,错误的是( )
A、已知函数f(x)=
| ||
B、设回归直线方程为
| ||
| C、已知ξ服从正态分布 N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.1 | ||
| D、对于命题p:“?x∈R,x2+x+1<0”,则?p:“?x∈R,x2+x+1>0” |

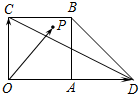 如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设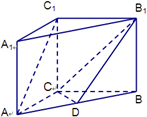 如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1(侧棱与底面垂直的棱柱称为直棱柱)中,AC=CC1=3,BC=4,AB=5,点D是AB的中点.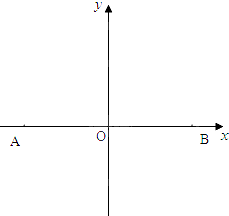 如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)
如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)