题目内容
某人在同一城市开了两家小店,每家店各有2名员工.节日期间,每名员工请假的概率都是
,且是否请假互不影响.若某店的员工全部请假,而另一家店没有人请假,则调剂1人到该店以维持正常运转,否则该店就关门停业.计算:
(Ⅰ)有人被调剂的概率;
(Ⅱ)停业的店铺数X的分布列和数学期望.
| 1 |
| 2 |
(Ⅰ)有人被调剂的概率;
(Ⅱ)停业的店铺数X的分布列和数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)根据题意,设出事件列出概率运用公式求解.
(Ⅱ)求出X的可能取值为0,1,2.分别求解概率,列出分布列求出数学期望,
(Ⅱ)求出X的可能取值为0,1,2.分别求解概率,列出分布列求出数学期望,
解答:
解 (Ⅰ)设某人所开的两家小店分别为A和B,
分别记A、B的员工全部请假为事件A0、B0,A、B的员工有1人,
没有请假为事件A1、B1,A、B的员工都没有请假为事件A2、B2,A、B的员工至少有1人没有请假为事件A3、B3.
由已知有,P ( A0 )=P ( B0 )=(
)2=
,
P ( A1 )=P ( B1 )=
• (
)2=
,
P ( A2 )=P ( B2 )=(
)2=
,
P ( A3 )=P ( B3 )=1-(
)2=
,
有人被调剂的概率为P ( A0 B2+A2B0 )=P ( A0 ) P ( B2 )+P ( A2 ) P ( B0 )=2×
×
=
.
(Ⅱ)X的可能取值为0,1,2.
P(X=0)=P(A3B3+A0B2+A2B0)=P(A3)P(B3)+P(A0B2+A2B0)=
×
+
=
,P ( X=1 )=P ( A0B1+A1B0 ) =P ( A0 ) P ( B1 )+P ( A1 ) P ( B0 )=2×
×
=
,P ( X=2 )=P ( A0B0 ) =P ( A0 ) P ( B0 ) =
×
=
.
所以,X的分布列是
X的数学期望EX=0×
+1×
+2×
=
.
分别记A、B的员工全部请假为事件A0、B0,A、B的员工有1人,
没有请假为事件A1、B1,A、B的员工都没有请假为事件A2、B2,A、B的员工至少有1人没有请假为事件A3、B3.
由已知有,P ( A0 )=P ( B0 )=(
| 1 |
| 2 |
| 1 |
| 4 |
P ( A1 )=P ( B1 )=
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
P ( A2 )=P ( B2 )=(
| 1 |
| 2 |
| 1 |
| 4 |
P ( A3 )=P ( B3 )=1-(
| 1 |
| 2 |
| 3 |
| 4 |
有人被调剂的概率为P ( A0 B2+A2B0 )=P ( A0 ) P ( B2 )+P ( A2 ) P ( B0 )=2×
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
(Ⅱ)X的可能取值为0,1,2.
P(X=0)=P(A3B3+A0B2+A2B0)=P(A3)P(B3)+P(A0B2+A2B0)=
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 8 |
| 11 |
| 16 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
所以,X的分布列是
| X | 0 | 1 | 2 | ||||||
| p |
|
|
|
| 11 |
| 16 |
| 1 |
| 4 |
| 1 |
| 16 |
| 3 |
| 8 |
点评:本题考查了离散型随机变量的概率,分布列,数学期望,属于中档题.

练习册系列答案
相关题目
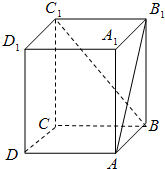
如图:正方体ABCD-A1B1C1D1中,AB1与C1B所成的角为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
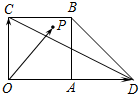 如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设