题目内容
记关于x的不等式(x-a)(x+1)<0的解集为P,不等式x2-2x≤0的解集为Q.
(Ⅰ)若a=3,求P;
(Ⅱ)若Q⊆P,求正数a的取值范围.
(Ⅰ)若a=3,求P;
(Ⅱ)若Q⊆P,求正数a的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:(1)把a=3代入不等式解集合P;
(2)根据Q⊆P,求正数a的取值范围.
(2)根据Q⊆P,求正数a的取值范围.
解答:
解:(I)当a=3时,由(x-3)(x+1)<0,得P=(-1,3)…4分
(II)由Q={x|0≤x≤2}…6分
由a>0,得P=(-1,a),…8分
又Q⊆P,所以a>2,
即a的取值范围是(2,+∞)…10分.
(II)由Q={x|0≤x≤2}…6分
由a>0,得P=(-1,a),…8分
又Q⊆P,所以a>2,
即a的取值范围是(2,+∞)…10分.
点评:本题主要考查不等式的解法和集合间的关系.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
某中学拟安排6名实习老师到高一年级的3个班实习,每班2人,则甲在一班、乙不在一班的不同分配方案共有( )
| A、12种 | B、24种 |
| C、36种 | D、48种 |
已知4tan
=1-tan2
,则tanα的值为( )
| α |
| 2 |
| α |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知正项等比数列{an}中 a2•a6=4,则log2a1+log2a2+…+log2a7=( )
| A、5 | B、6 | C、7 | D、8 |
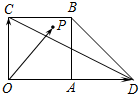 如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设