题目内容
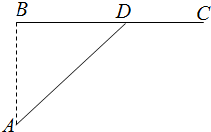 如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?
考点:解三角形的实际应用
专题:应用题,解三角形
分析:(1)用θ表示出AD与BD,从而可以表示出DC,由路程除以速度得时间,建立起时间关于θ函数即可;
(2)对函数求导,研究出函数的单调性确定出θ=
时,由A到C所用的时间t最少.
(2)对函数求导,研究出函数的单调性确定出θ=
| π |
| 3 |
解答:
解:(1)在Rt△ABD中,AB=50km,∴BD=50cotθ,AD=
,∴DC=100-BD=100-50cotθ.
∴t(θ)=
+2-cotθ=
+2(θ∈[arctan
,
));
(2)t′(θ)=
,
∴θ∈[0,
)时,t′(θ)<0;θ∈(
,
),t′(θ)>0
∴当θ=
时,由A到C所用的时间t最少.
| 50 |
| sinθ |
∴t(θ)=
| 2 |
| sinθ |
| 2-cosθ |
| sinθ |
| 1 |
| 2 |
| π |
| 2 |
(2)t′(θ)=
| 1-2cosθ |
| sin2θ |
∴θ∈[0,
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
∴当θ=
| π |
| 3 |
点评:本题考查在实际问题中建立三角函数模型,应用三角函数模型求解用时最少的问题,求解本题的关键是对问题进行细致分析得出符合条件的函数模型.

练习册系列答案
相关题目
已知4tan
=1-tan2
,则tanα的值为( )
| α |
| 2 |
| α |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
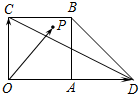 如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设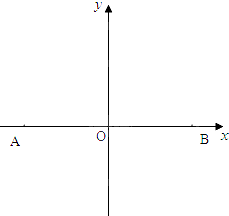 如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)
如图,A,B两地相距10km,A(-5,0),B(5,0).有一种商品,A、B两地均有出售且价格相同,某地居民从两地之一购得商品运回来,每公里的运费A地是B地的3倍.问该地居民应如何选择A地或B地购买此种商品最合算?(仅从运费的多少来考虑)