题目内容
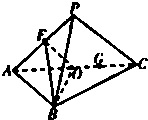 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,O分别为PA,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,O分别为PA,AC的中点,AC=16,PA=PC=10.(1)求BP与平面BOE所成角的正弦值;
(2)若G是OC的中点,在棱PB上是否存在点F,使得GF∥平面BOE,若存在,求PF:FB;若不存在,请说明理由.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)首先根据面面的垂直关系转化为线线垂直,然后建立直角坐标系,利用法向量求出线面的夹角的正弦值.
(2)先假设存在然后进行证明,利用相面的平行关系,建立向量与法向量之间的联系,最终求出结果.
(2)先假设存在然后进行证明,利用相面的平行关系,建立向量与法向量之间的联系,最终求出结果.
解答:
解:(1)连结PO,
因为:PA=PC,O是AC的中点,
∴PO⊥AC
由平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
∴PO⊥平面ABC,
PO⊥OB,PO⊥OC
△ABC是以AC为斜边的等腰直角三角形,O是AC的中点
∴BO⊥AC
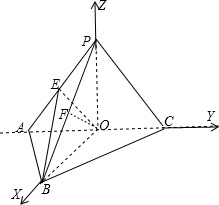
分别以OB,OC,OP所在的直线建立x轴y轴和z轴
进一步求得:A(0,-8,0),B(8,0,0),C(0,8,0),P(0,0,6),E(0,-4,3)
设平面OBE得法向量为:
=(x,y,z)
则:
令y=3则z=4
所以:
=(0,3,4)
设BP与平面BOE所成的角为θ
sinθ=|
|=
(2)假设在棱PB上是否存在点F,使得GF∥平面BOE,进一步
=λ
(0≤λ≤1)
G(0,4,0),
=
+
+
=(8-8λ,-4,6λ)
由于GF∥平面BOE,
所以
•
=3×(-4)+4×6λ=0
解得:λ=
所以
=1
因为:PA=PC,O是AC的中点,
∴PO⊥AC
由平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
∴PO⊥平面ABC,
PO⊥OB,PO⊥OC
△ABC是以AC为斜边的等腰直角三角形,O是AC的中点
∴BO⊥AC
分别以OB,OC,OP所在的直线建立x轴y轴和z轴
进一步求得:A(0,-8,0),B(8,0,0),C(0,8,0),P(0,0,6),E(0,-4,3)
设平面OBE得法向量为:
| n |
则:
|
令y=3则z=4
所以:
| n |
设BP与平面BOE所成的角为θ
sinθ=|
| ||||
|
|
| 12 |
| 25 |
(2)假设在棱PB上是否存在点F,使得GF∥平面BOE,进一步
| BF |
| BP |
G(0,4,0),
| GF |
| GO |
| OB |
| BF |
由于GF∥平面BOE,
所以
| GF |
| n |
解得:λ=
| 1 |
| 2 |
所以
| PF |
| FB |

点评:本题考查的知识点:面面垂直与线面垂直的转化和线线垂直之间的转化,法向量的应用,空间直角坐标系的建立,线面的夹角的应用,向量的夹角的应用,存在性问题的确定.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
下列四个命题中,错误的是( )
A、已知函数f(x)=
| ||
B、设回归直线方程为
| ||
| C、已知ξ服从正态分布 N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.1 | ||
| D、对于命题p:“?x∈R,x2+x+1<0”,则?p:“?x∈R,x2+x+1>0” |
 有一个容量为200的样本,其频率分布直方图如图所示,据图估计,样本数据在[8,10)内的频数为
有一个容量为200的样本,其频率分布直方图如图所示,据图估计,样本数据在[8,10)内的频数为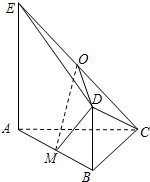 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=
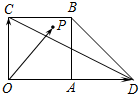 如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设
如图,四边形OABC是边长为1的正方形,点D在OA的延长线上,且OD=2,点P为△BCD内(含边界)的动点,设