题目内容
定义:[x](x∈R)表示不超过x的最大整数.例如[1.5]=1,[-0.5]=-1.给出下列结论:
①函数y=[sinx]是奇函数;
②函数y=[sinx]是周期为2π的周期函数;
③函数y=[sinx]-cosx不存在零点;
④函数y=[sinx]+[cosx]的值域是{-2,-1,0,1}.
其中正确的是 .(填上所有正确命题的编号)
①函数y=[sinx]是奇函数;
②函数y=[sinx]是周期为2π的周期函数;
③函数y=[sinx]-cosx不存在零点;
④函数y=[sinx]+[cosx]的值域是{-2,-1,0,1}.
其中正确的是
考点:命题的真假判断与应用
专题:综合题,新定义,推理和证明
分析:利用新定义,对4个命题分别进行判断,即可得出结论.
解答:
解:①函数y=[sinx]是非奇非偶函数;
②函数y=[sinx]的周期与y=sinx的周期相同,故是周期为2π的周期函数;
③函数y=[sinx]的取值是-1,0,1,故y=[sinx]-cosx不存在零点;
④函数数y=[sinx]、y=[cosx]的取值是-1,0,1,故y=[sinx]+[cosx]的值域是{-2,-1,0,1}.
故答案为:②③④.
②函数y=[sinx]的周期与y=sinx的周期相同,故是周期为2π的周期函数;
③函数y=[sinx]的取值是-1,0,1,故y=[sinx]-cosx不存在零点;
④函数数y=[sinx]、y=[cosx]的取值是-1,0,1,故y=[sinx]+[cosx]的值域是{-2,-1,0,1}.
故答案为:②③④.
点评:本题考查命题的真假判断,考查新定义,正确理解新定义是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
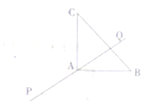 如图,在Rt△ABC中,|
如图,在Rt△ABC中,|
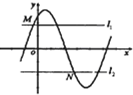 如图:M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m,l2:y=-m(A≥m≥0)的两个交点,记S=|xN-xM|,则S(m)图象大致是( )
如图:M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m,l2:y=-m(A≥m≥0)的两个交点,记S=|xN-xM|,则S(m)图象大致是( )



