题目内容

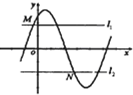如图：M（xM，yM），N（xN，yN）分别是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与两条直线l1：y=m，l2：y=-m（A≥m≥0）的两个交点，记S=|xN-xM|，则S（m）图象大致是（　　）
A、
B、
C、
D、
考点：函数的图象
专题：函数的性质及应用
分析：从已知条件及所给函数的图象出发，图象从M点到N点的变化正好是半个周期，故xN-xM=
T
2
，则在一个周期内S=|xN-xM|=常数，只有C符合．
解答： 解：由已知条件及所给函数的图象知，图象从M点到N点的变化正好是半个周期，
故xN-xM=
T
2
，则在一个周期内S=|xN-xM|=常数，只有C符合，
故选：C．
点评：本题主要考查函数的图象性质，结合三角函数的周期性考查学生，属于基础题．
练习册系列答案
相关题目
设点M是线段BC的中点，点A在直线BC外，|
BC
|=4，|
AB
+
AC
|=|
AB
-
AC
|，则
AM
•(
AB
+
AC
)=（　　）
A、8B、4C、2D、1
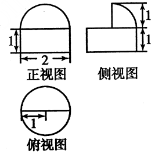
一个几何体的三视图如图所示，则该几何体的体积为（　　）
A、
2π
3
B、
4π
3
C、
3π
4
D、
3π
2
某网站有10种资料，下载这些资料需要储值或点数，其中3种资料是精品资料，下载一个需扣5个储值，7种普通资料下载一个需扣4个点．某人现有20个点与10个储值，准备下载6种资料（每种资料至多下载一个，储值只用于下载精品资料，点只用于下载普通资料，点与储值够用即可，不必用完），则不同的下载方法的种数是（　　）
A、62B、105
C、168D、231．
已知数列{an}中，a1=1，an+1=
1
3
an+n，n为奇数
an-3n，n为偶数

（I）证明数列{a2n-
3
2
}是等比数列；
（II）若Sn是数列{an}的前n项和，求S2n．
定义：[x]（x∈R）表示不超过x的最大整数．例如[1.5]=1，[-0.5]=-1．给出下列结论：
①函数y=[sinx]是奇函数；
②函数y=[sinx]是周期为2π的周期函数；
③函数y=[sinx]-cosx不存在零点；
④函数y=[sinx]+[cosx]的值域是{-2，-1，0，1}．
其中正确的是
 
．（填上所有正确命题的编号）
若双曲线C：
x2
a2
-
y2
b2
=1的一条渐近线的倾斜角为
π
6
，则双曲线C的离心率为（　　）
A、2或
3
B、
2
3
3
C、2或
2
3
3
D、2
设函数f（x）=x2+2bx+c（c＜b＜1）的一个零点是1，且函数g（x）=f（x）+1也有零点．
（1）证明：-3＜c≤-1，且b≥0；
（2）若m是函数g（x）的一个零点，试判断f（m-4）的正负，并加以证明．
已知sin2a=
1
3
，则
1
tana
-
1
tan2a
的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网