题目内容
已知函数f(x)=4cosωx•sin(ωx+
)+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
| π |
| 6 |
(Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
考点:正弦函数的单调性,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:(Ⅰ)根据条件确定函数最值和周期,利用三角函数的公式进行化简即可求a和ω的值;
(Ⅱ)根据三角函数的单调性即可求出函数的单调递减区间.
(Ⅱ)根据三角函数的单调性即可求出函数的单调递减区间.
解答:
解:(Ⅰ)f(x)=4cosωx•sin(ωx+
)+a=4cosωx•(
sinωx+
cosωx)+a=2
sinωxcosωx+2cos2ωx-1+1+a=
sin2ωx+cos2ωx+1+a=2sin(2ωx+
)+1+a.
当sin(2ωx+
)=1时,f(x)取得最大值2+1+a=3+a
又f(x)最高点的纵坐标为2,
∴3+a=2,即a=-1.
又f(x)图象上相邻两个最高点的距离为π,
∴f(x)的最小正周期为T=π
故2ω=
=2,ω=1
(Ⅱ)由(Ⅰ)得f(x)=2sin(2x+
)
由
+2kπ≤2x+
≤
+2kπ,k∈Z.
得
+kπ≤x≤
+kπ,k∈Z.
令k=0,得:
≤x≤
.
故函数f(x)在[0,π]上的单调递减区间为[
,
]
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| π |
| 6 |
当sin(2ωx+
| π |
| 6 |
又f(x)最高点的纵坐标为2,
∴3+a=2,即a=-1.
又f(x)图象上相邻两个最高点的距离为π,
∴f(x)的最小正周期为T=π
故2ω=
| 2π |
| T |
(Ⅱ)由(Ⅰ)得f(x)=2sin(2x+
| π |
| 6 |
由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
得
| π |
| 6 |
| 2π |
| 3 |
令k=0,得:
| π |
| 6 |
| 2π |
| 3 |
故函数f(x)在[0,π]上的单调递减区间为[
| π |
| 6 |
| 2π |
| 3 |
点评:本题主要考查三角函数的图象和性质,利用三角函数的图象以及三角函数的辅助角公式求出函数的解析式是解决本题的关键.

练习册系列答案
相关题目
复数
(i是虚数单位)的虚部是( )
| 1 |
| i-1 |
| A、1 | ||
| B、i | ||
C、-
| ||
D、
|
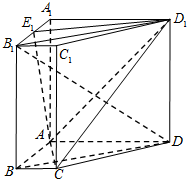 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=