题目内容
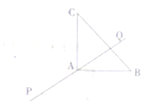 如图,在Rt△ABC中,|
如图,在Rt△ABC中,|| PA |
| BC |
| PA |
| 1 |
| 2 |
| PQ |
| PQ |
| BC |
| CP |
| BQ |
考点:平面向量数量积的运算
专题:三角函数的图像与性质,平面向量及应用
分析:以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角坐标系.求出各顶点的坐标后,进而给出向量
,
的坐标,然后利用平面向量的数量值运算公式,构造一个关于cosθ的式子,然后根据cosθ的取值范围,分析出
•
的最大值.
| BP |
| CQ |
| BP |
| CQ |
解答:
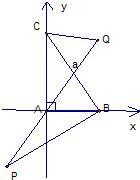 解:以直角顶点A为坐标原点,
解:以直角顶点A为坐标原点,
两直角边所在直线为坐标轴建立如图所示的平面直角坐标系.
设|AB|=c,|AC|=b,则A(0,0),B(c,0),C(0,b),
且|PQ|=2a,|BC|=a.
设点P的坐标为(x,y),则Q(-x,-y).
∴
=(x-c,y),
=(-x,-y-b),
=(-c,b),
=(-2x,-2y).
∴
•
=(x-c)•(-x)+y(-y-b)=-(x2+y2)+cx-by=-a2+cx-by.
∵cosθ=
=
.
∴cx-by=a2cosθ.
∴
•
=-a2+a2cosθ.
故当cosθ=1,即θ=0(
与
方向相同)时,
•
最大,其最大值为0.
 解:以直角顶点A为坐标原点,
解:以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角坐标系.
设|AB|=c,|AC|=b,则A(0,0),B(c,0),C(0,b),
且|PQ|=2a,|BC|=a.
设点P的坐标为(x,y),则Q(-x,-y).
∴
| BP |
| CQ |
| BC |
| PQ |
∴
| BP |
| CQ |
∵cosθ=
| ||||
|
|
| cx-by |
| a2 |
∴cx-by=a2cosθ.
∴
| BP |
| CQ |
故当cosθ=1,即θ=0(
| PQ |
| BC |
| BP |
| CQ |
点评:本题主要考查向量的数量积的坐标表示和性质等概念,平面向量的运算法则,考查运用向量及三角函数的值域的能力.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A、100 cm3 |
| B、108 cm3 |
| C、84 cm3 |
| D、92 cm3 |
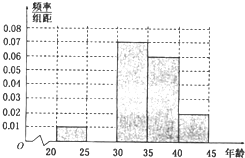 在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,据此估计这800名志愿者年龄在[25,30)的人数为
在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,据此估计这800名志愿者年龄在[25,30)的人数为