题目内容
某单位为了了解办公楼用电量y(度)与气温x(℃)之间的关系,随机统计了四个工作量与当天平均气温,并制作了对照表:
由表中数据得到线性回归方程
=-2x+a,当气温为-4℃时,预测用电量均为( )
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
 |
| y |
| A、68度 | B、52度 |
| C、12度 | D、28度 |
考点:线性回归方程
专题:概率与统计
分析:根据所给的表格做出本组数据的样本中心点,根据样本中心点在线性回归直线上,利用待定系数法做出a的值,可得线性回归方程,根据所给的x的值,代入线性回归方程,预报要销售的件数.
解答:
解:由表格得
=
(18+13+10-1)=10,
(24+34+38+64)=40.
∴(
,
)为:(10,40),
又(
,
)在回归方程
=bx+a中的b=-2,
∴40=10×(-2)+a,
解得:a=60,
∴
=-2x+60,
当x=-4时,
=-2×(-4)+60=68.
故选:A.
. |
| x |
| 1 |
| 4 |
| y |
| 1 |
| 4 |
∴(
. |
| x |
. |
| y |
又(
. |
| x |
. |
| y |
| ? |
| y |
∴40=10×(-2)+a,
解得:a=60,
∴
| ? |
| y |
当x=-4时,
| ? |
| y |
故选:A.
点评:本题考查线性回归方程,考查最小二乘法的应用,考查利用线性回归方程预报变量的值,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
某网站有10种资料,下载这些资料需要储值或点数,其中3种资料是精品资料,下载一个需扣5个储值,7种普通资料下载一个需扣4个点.某人现有20个点与10个储值,准备下载6种资料(每种资料至多下载一个,储值只用于下载精品资料,点只用于下载普通资料,点与储值够用即可,不必用完),则不同的下载方法的种数是( )
| A、62 | B、105 |
| C、168 | D、231. |
若双曲线C:
-
=1的一条渐近线的倾斜角为
,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、2或
| ||||
B、
| ||||
C、2或
| ||||
| D、2 |
已知函数f(x)=
,则满足f(a)≥2的实数a的取值范围是( )
|
| A、(-∞,-2)∪(0,+∞) |
| B、(-1,0) |
| C、(-2,0) |
| D、(-∞,-1]∪[0,+∞) |
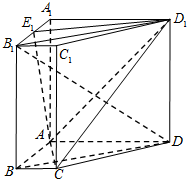 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=