题目内容

求证：
sina-cosa+1
sina+cosa-1
=
cosa
1-sina
．
考点：三角函数恒等式的证明
专题：三角函数的求值
分析：利用分析法将比例式化为等积式，然后展开化简，得到等式．
解答： 证明：要证明
sina-cosa+1
sina+cosa-1
=
cosa
1-sina
，
只要证明（sinα-cosα+1）（1-sinα）=（sinα+cosα-1）cosα，
即证sinα-sin2α-cosα+cosαsinα+1-sinα=sinαcosα+cos2α-cosα
即证cos2α-cosα+sinαcosα=sinαcosα+cos2α-cosα
此等式成立；
所以原等式成立．
点评：本题考查了利用分析法证明三角恒等式．
练习册系列答案
相关题目
已知A（-1，cosθ），B（sinθ，1），若|
OA
+
OB
|=|
OA
-
OB
|（O为坐标原点），则锐角θ=
 
．
定义：[x]（x∈R）表示不超过x的最大整数．例如[1.5]=1，[-0.5]=-1．给出下列结论：
①函数y=[sinx]是奇函数；
②函数y=[sinx]是周期为2π的周期函数；
③函数y=[sinx]-cosx不存在零点；
④函数y=[sinx]+[cosx]的值域是{-2，-1，0，1}．
其中正确的是
 
．（填上所有正确命题的编号）
已知函数f（x）=
2-2x，x≤-1
2x+2，x＞-1
，则满足f（a）≥2的实数a的取值范围是（　　）
A、（-∞，-2）∪（0，+∞）
B、（-1，0）
C、（-2，0）
D、（-∞，-1]∪[0，+∞）
设函数f（x）=x2+2bx+c（c＜b＜1）的一个零点是1，且函数g（x）=f（x）+1也有零点．
（1）证明：-3＜c≤-1，且b≥0；
（2）若m是函数g（x）的一个零点，试判断f（m-4）的正负，并加以证明．
运行如如图所示的程序框图，则输出的结果S为（　　）
A、1008B、2015
C、1007D、-1007
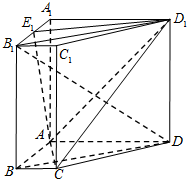如图，在四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，底面ABCD是直角梯形，AD∥BC，∠BAD=90°，BC=1，AB=
3
，AD=AA1=3，E1为A1B1中点．
（Ⅰ）证明：B1D∥平面AD1E1；
（Ⅱ）证明：平面ACD1⊥平面BDD1B1．
已知函数f（x）=2x2+4（a-3）x+5在区间（-8，-3）上是减函数，则a的取值范围是
 
．
求下列函数的导数：
（1）y=cos(
π
3
-4x)
（2）y=2(xex+e-
1
2
)
（3）y=
sin2x
2x-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网