题目内容
已知一个容量为40的数据样本，分组后，组距与频率如下：[20，30），4个；[30，40），6个；[40，50），8个；[50，60），9个[60，70），7个；[70，80），6个．则样本在区间[60，+∞）上的频率是（ ）
| A、10% | B、20% |
| C、32.5% | D、40% |
考点：频率分布直方图
专题：概率与统计
分析：求出样本在区间[60，+∞）上的频数，利用频率=
，求出对应的频率是多少．
| 频数 |
| 样本容量 |
解答：
解：根据题意，
样本在区间[60，+∞）上的频数是
40-4-6-8-9=13；
∴对应的频率是
=32.5%．
故选：C．
样本在区间[60，+∞）上的频数是
40-4-6-8-9=13；
∴对应的频率是
| 13 |
| 40 |
故选：C．
点评：本题考查了频率的计算问题，解题时利用频率公式进行计算即可，是基础题．
练习册系列答案
相关题目
若平面α∥平面β，直线a∥平面α，点B∈β，则在平面β内且过B点的所有直线中（ ）
| A、不一定存在与a平行的直线 |
| B、只有两条与a平行的直线 |
| C、存在无数条与a平行的直线 |
| D、存在唯一与a平行的直线 |
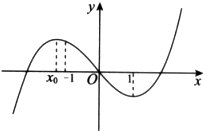函数f（x）=ax3-bx2+cx的图象如图所示，且f（x）在x=x0与x=1处取得极值，给出下列判断：①c＞0；
②f（1）+f（-1）＞0；
③函数y=f′（x）在区间（0，+∞）上是增函数．
其中正确的判断是（ ）
| A、①③ | B、② | C、②③ | D、①② |
命题“对任意实数x，都有x＞1”的否定是（ ）
| A、对任意实数x，都有x＜1 |
| B、不存在实数x，使x≤1 |
| C、对任意实数x，都有x≤1 |
| D、存在实数x，使x≤1 |
已知x，y满足约束条件
，则目标函数z=2x+y的最大值是（ ）
|
A、
| ||
B、2
| ||
C、
| ||
D、2
|
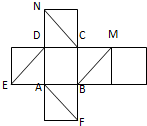如图是正方体的平面展开图，在这个正方体中；（1）CN与AF平行；
（2）CN与BE是异面直线；
（3）CN与BM成60°；
（4）DE与BM垂直．
以上四个命题中，正确命题的序号是（ ）
| A、（1）（2）（3） |
| B、（2）（4） |
| C、（3）（4） |
| D、（3） |
如图为正方体表面的一种展开图，则图中的四条线段AB，CD，EF，GH在原正方体中互为异面的对数为（ ）| A、1 | B、2 | C、3 | D、4 |