题目内容
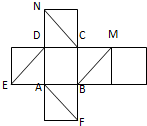如图是正方体的平面展开图，在这个正方体中；（1）CN与AF平行；
（2）CN与BE是异面直线；
（3）CN与BM成60°；
（4）DE与BM垂直．
以上四个命题中，正确命题的序号是（ ）
| A、（1）（2）（3） |
| B、（2）（4） |
| C、（3）（4） |
| D、（3） |
考点：空间中直线与直线之间的位置关系
专题：综合题,空间位置关系与距离
分析：把展开图再还原成正方体如图所示：（1）CN与AF是异面直线；（2）CN与BE是平行；（3）由于BE和CN平行且相等，故∠EBM（或其补角）为所求．再由△BEM是等边三角形，可得∠EBM=60°；（4）DE与BM是异面直线且垂直．
解答：
解：把展开图再还原成正方体如图所示：
（1）CN与AF是异面直线，故不正确；
（2）CN与BE是平行，故不正确；
（3）由于BE和CN平行且相等，故异面直线CN与BM所成的角就是BE和BM所成的角，故∠EBM（或其补角）为所求，再由△BEM是等边三角形，可得∠EBM=60°，故正确；
（4）DE与BM是异面直线且垂直，故正确．
故选：C．
解：把展开图再还原成正方体如图所示：（1）CN与AF是异面直线，故不正确；
（2）CN与BE是平行，故不正确；
（3）由于BE和CN平行且相等，故异面直线CN与BM所成的角就是BE和BM所成的角，故∠EBM（或其补角）为所求，再由△BEM是等边三角形，可得∠EBM=60°，故正确；
（4）DE与BM是异面直线且垂直，故正确．
故选：C．
点评：本题主要考查求异面直线所成的角，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
下列哪个函数与y=x是相同函数（ ）
A、y=
| |||
B、y=
| |||
C、y=
| |||
| D、y=alogax（a＞0且a≠1） |
设a，b，c∈（-∞，0），则a+
，b+
，c+
（ ）
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
| A、都不大于-4 |
| B、都不小于-4 |
| C、至少有一个不大于-4 |
| D、至少有一个不小于-4 |
已知从A口袋中摸出一个球是红球的概率为
，从B口袋中摸出一个球是红球的概率为
．现从两个口袋中各摸出一个球，那么这两个球中没有红球的概率是（ ）
| 1 |
| 3 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知一个容量为40的数据样本，分组后，组距与频率如下：[20，30），4个；[30，40），6个；[40，50），8个；[50，60），9个[60，70），7个；[70，80），6个．则样本在区间[60，+∞）上的频率是（ ）
| A、10% | B、20% |
| C、32.5% | D、40% |
已知二次函数y=2x2-1在区间[a，b]上有最小值-1，则下面关系一定成立的是（ ）
| A、a≤0＜b或a＜0≤b |
| B、a＜0＜b |
| C、a＜b＜0或a＜0＜b |
| D、0＜a＜b或a＜b＜0 |
当θ是第四象限时，两直线xsinθ+y
-a=0和x+y
+b=0的位置关系是（ ）
| 1+cosθ |
| 1-cosθ |
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、重合 |
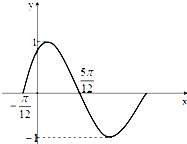函数y=Asin（ωx+Φ）（A＞0，ω＞0，|Φ|＜