题目内容

已知?ABCD的顶点A（-3，-2），B（3，-4），C（6，0）．
（Ⅰ）求顶点D的坐标；
（Ⅱ）求
AB
在
AD
方向上的投影．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（Ⅰ）设顶点D的坐标为（x，y），则由题意可得
AB
=
DC
 求得x、y的值，可得点D的坐标．
（Ⅱ）求出
AB
、
AD
 的坐标，可得 
AB
•
AD
 和|
AD
|的值，再根据
AB
在
AD
方向上的投影为|
AB
|•cos∠BAD=|
AB
|•
AB
•
AD
|
AB
|•|
AD
|
，求出结果．
解答： 解：（Ⅰ）设顶点D的坐标为（x，y），则由题意可得
AB
=
DC
，∴（6，-2）=（6-x，-y），
∴
6-x=6
-2=-y
，求得
x=0
y=2
，可得点D的坐标为（0，2）．
（Ⅱ）∵
AB
=（6，-2），
AD
=（3，4），∴
AB
•
AD
=18-8=10，|
AD
|=5，
∴
AB
在
AD
方向上的投影为|
AB
|•cos∠BAD=|
AB
|•
AB
•
AD
|
AB
|•|
AD
|
=
AB
•
AD
|
AD
|
=
10
5
=2．
点评：本题主要考查两个向量的数量积公式，两个向量坐标形式的运算，属于基础题．
练习册系列答案
相关题目
如图是计算y=f（x）函数值的程序框图．   
（Ⅰ）请写出程序对应函数f（x）的表达式；
（Ⅱ）若输出的结果是正数，求输入的实数x的取值范围．
过点A（-2，m）和B（m，4）的直线与直线l：x-2y-1=0垂直，则m的值为（　　）
A、10B、2C、0D、-8
若x
1
3
+x-
1
3
=3，则x+x-1=
 
．
已知点M（a，b）（ab≠0）是圆x2+y2=r2内一点，直线g是以M为中点的弦所在直线，直线l的方程为ax+by+r2=0，则直线l（　　）
A、l∥g，且与圆相切
B、l∥g，且与圆相离
C、l⊥g，且与圆相切
D、l⊥g，且与圆相离
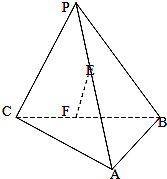如图，E、F分别是三棱锥P-ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为（　　）
A、120°B、45°
C、0°D、60°
设关于x，y的不等式组
3x-y+1＞0
x+3m＜0
y-m＞0
表示的平面区域内存在点P（x0，y0），满足x0-3y0=3，求得m的取值范围是（　　）
A、（-∞，-
1
3
）
B、（-∞，
1
3
）
C、（-∞，-
1
2
）
D、（-∞，
1
2
）
若a，b，c∈R，a＞b，则下列不等式成立的是（　　）
A、
a
c2+1
＞
b
c2+1
B、a2＞b2
C、
1
a
＜
1
b
D、a|c|＞b|c|
sin840°等于（　　）
A、-
1
2
B、
3
2
C、-
3
2
D、
1
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网