题目内容
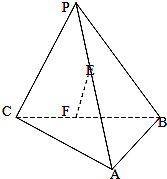如图，E、F分别是三棱锥P-ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为（ ）| A、120° | B、45° |
| C、0° | D、60° |
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：先取AC的中点G，连接EG，GF，由三角形的中位线定理可得GE∥PC，GF∥AB且GB=5，GF=3，根据异面直线所成角的定义，再利用余弦定理求解．
解答：
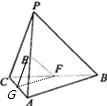解：取AC的中点G，连接EG，GF，
由中位线定理可得：GE∥PC，GF∥AB且GB=5，GF=3，
∴∠EGF是异面直线PC，AB所成的角，
在△GBF中由余弦定理可得：cos∠EGF=
=
，∴∠EGF=60°，
故选：D．
解：取AC的中点G，连接EG，GF，由中位线定理可得：GE∥PC，GF∥AB且GB=5，GF=3，
∴∠EGF是异面直线PC，AB所成的角，
在△GBF中由余弦定理可得：cos∠EGF=
| EG2+FG2-EF2 |
| 2EG•FG |
| 1 |
| 2 |
故选：D．
点评：本题主要考查空间几何体的结构特征和异面直线所成的角的求法，同时，还考查了转化思想和运算能力，属中档题．
练习册系列答案
相关题目
| 2 |
| 2 |
| A、1 | B、±1 |
| C、-1 | D、以上选项都不对 |
函数y=f（x）在区间（-1，1）上是减函数，且f（1-a）＜f（2a-1），则a的取值范围为（ ）
A、(
| ||
B、(-∞，
| ||
C、(0，
| ||
D、(
|
过双曲线
-
=1（a＞0，b＞0）的右焦点F和虚轴的一端点B作一条直线，若右顶点A到直线FB的距离为
，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| b | ||
|
A、
| ||||
| B、2 | ||||
C、2
| ||||
D、2或
|
若tanα=-
，则
的值是（ ）
| 1 |
| 2 |
| 1+2sinαcosα |
| sin2α-cos2α |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |