题目内容
过点A（-2，m）和B（m，4）的直线与直线l：x-2y-1=0垂直，则m的值为（ ）
| A、10 | B、2 | C、0 | D、-8 |
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：由直线方程可得斜率，进而又垂直关系和斜率公式可得m的方程，解方程可得．
解答：
解：∵直线l：x-2y-1=0的斜率为
，
由直线的垂直关系可得AB的斜率为-2，
∴由斜率公式可得
=-2，
解得m=-8
故选：D
| 1 |
| 2 |
由直线的垂直关系可得AB的斜率为-2，
∴由斜率公式可得
| m-4 |
| -2-m |
解得m=-8
故选：D
点评：本题考查直线的一般式方程和垂直关系，属基础题．
练习册系列答案
相关题目
在△ABC中，角A，B，C的对边分别是a，b，c，若A：B：C=1：2：3，则a：b：c=（ ）
| A、1：2：3 | ||
| B、2：3：4 | ||
| C、3：4：5 | ||
D、1：
|
对数lg(
+
)的值为（ ）
3+
|
3-
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
函数y=f（x）在区间（-1，1）上是减函数，且f（1-a）＜f（2a-1），则a的取值范围为（ ）
A、(
| ||
B、(-∞，
| ||
C、(0，
| ||
D、(
|
若关于x的方程ax2-2x+1=0的解集中有且仅有一个元素，则实数a的值组成的集合中的元素个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
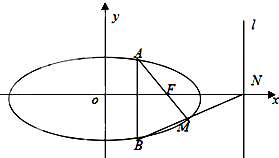如图，已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点，且椭圆C上的点到点F的最大距离为3．