题目内容
已知点M(a,b)(ab≠0)是圆x2+y2=r2内一点,直线g是以M为中点的弦所在直线,直线l的方程为ax+by+r2=0,则直线l( )
| A、l∥g,且与圆相切 |
| B、l∥g,且与圆相离 |
| C、l⊥g,且与圆相切 |
| D、l⊥g,且与圆相离 |
考点:轨迹方程
专题:计算题,直线与圆
分析:由条件求得直线l的斜率,再求出直线m的斜率,可得它们的斜率相等.利用点到直线的距离公式求得圆心C到直线m的距离大于半径,由此可得l∥m且m与圆c相离.
解答:
解:由题意可得a2+b2<r2,设圆心为C,且CM⊥直线g,故直线g的斜率为-
=-
,
由于直线l的方程为ax+by+r2=0,则l的斜率为-
,
圆心C到直线l的距离等于
>r,
故l∥g且l与圆c相离,
故选B.
| 1 |
| kCM |
| a |
| b |
由于直线l的方程为ax+by+r2=0,则l的斜率为-
| a |
| b |
圆心C到直线l的距离等于
| |0+0+r2| | ||
|
故l∥g且l与圆c相离,
故选B.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,属于中档题.

练习册系列答案
相关题目
化简
=( )
| 1-cos200° |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若关于x的方程ax2-2x+1=0的解集中有且仅有一个元素,则实数a的值组成的集合中的元素个数为( )
| A、1 | B、2 | C、3 | D、4 |
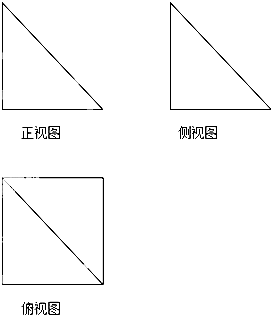 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是( ) 如图所示,某地一天从6~14时的温度变化曲线近似满足y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<π,b∈R),写出这段曲线的函数解析式
如图所示,某地一天从6~14时的温度变化曲线近似满足y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<π,b∈R),写出这段曲线的函数解析式