题目内容
设关于x,y的不等式组
表示的平面区域内存在点P(x0,y0),满足x0-3y0=3,求得m的取值范围是( )
|
A、(-∞,-
| ||
B、(-∞,
| ||
C、(-∞,-
| ||
D、(-∞,
|
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:先根据约束条件画出可行域.要使可行域存在,必有m<-9m+1,要求可行域包含直线y=
x-1上的点,只要边界点(-3m,1-9m)在直线y=
x-1的上方,且(-3m,m)在直线y=
x-1的下方,从而建立关于m的不等式组,解之可得答案.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:先根据约束条件
画出可行域,
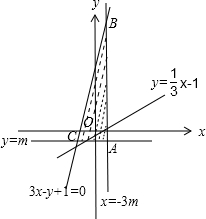
要使可行域存在,必有m<-9m+1,要求可行域包含直线y=
x-1上的点,只要边界点(-3m,1-9m)
在直线y=
x-1的上方,且(-3m,m)在直线y=
x-1的下方,
即
,解得:m<-
.
故选:C.
|

要使可行域存在,必有m<-9m+1,要求可行域包含直线y=
| 1 |
| 3 |
在直线y=
| 1 |
| 3 |
| 1 |
| 3 |
即
|
| 1 |
| 2 |
故选:C.
点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案,此题是中档题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
对数lg(
+
)的值为( )
3+
|
3-
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
若关于x的方程ax2-2x+1=0的解集中有且仅有一个元素,则实数a的值组成的集合中的元素个数为( )
| A、1 | B、2 | C、3 | D、4 |
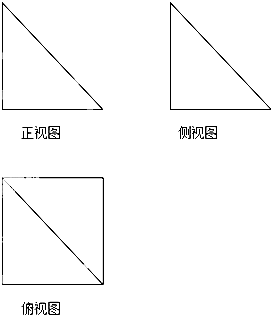 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是( )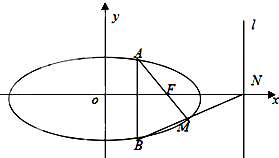 如图,已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为3.
如图,已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为3.