若a.b.c∈R.a＞b.则下列不等式成立的是( ) A.ac2+1＞bc2+1B.a2＞b2C.1a＜1bD.a|c|＞b|c| 题目和参考答案——青夏教育精英家教网—

题目内容

若a，b，c∈R，a＞b，则下列不等式成立的是（　　）

A、

c2+1

＞

c2+1

B、a²＞b²

C、

＜

D、a|c|＞b|c|

考点：不等式的基本性质

专题：不等式的解法及应用

分析：选项A，由不等式的性质可得，选项B，C，D举反例可推翻．

解答： 解：由题意可知a，b，c∈R，a＞b，
选项A，∵

c2+1

＞0，a＞b，∴

c2+1

＞

c2+1

，故正确；
选项B，取a=1，b=-2，显然满足a＞b，但a²＜b²，故错误；
选项C，仍取a=1，b=-2，显然满足a＞b，但

＞

，故错误；
选项D，当c=0时，显然a|c|=b|c|，故错误．
故选：A

点评：本题考查不等式的基本性质，属基础题．

练习册系列答案

，g （x）=x²，写出函数h（x）的解析式；
（2）求问题（1）中函数h（x）的值域；
（3）请设计一个定义域为R的函数y=f （x），及一个实常数a的值，使得f （x）•f （x+a）=x⁴+x²+1，并予证明．

已知?ABCD的顶点A（-3，-2），B（3，-4），C（6，0）．
（Ⅰ）求顶点D的坐标；
（Ⅱ）求

在

方向上的投影．

已知定义在（0，+∞）上的函数f（x），满足f（xy）=f（x）+f（y），且f（

）=1，对于x，y∈（0，+∞），当且仅当x＞y时f（x）＜f（y）．
（1）求f（1）的值；
（2）若f（-x）+f（3-x）≥-2，求x的取值范围．

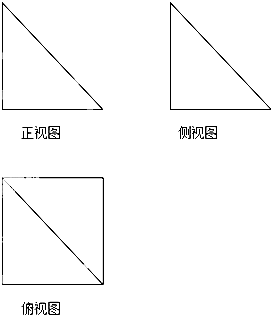一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是（　　）

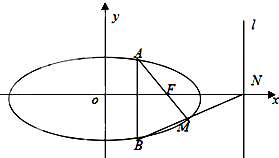如图，已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点，且椭圆C上的点到点F的最大距离为3．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若AB为垂直于x轴的动弦，直线l：x=4与x轴交于点N，直线AF与BN交于点M．
i．求证：点M恒在椭圆C上；
ii．求△AMN面积的最大值．

已知f（x）是以π为周期的偶函数，且x∈[0，

]时，f（x）=sin x-cosx．
（1）求当x∈[

π，3π]时f（x）的解析式．
（2）求不等式f（x）＜0的解集．

函数y=f（-x）的图象与函数y=f（4+x）的图象关于（　　）

试题分类